
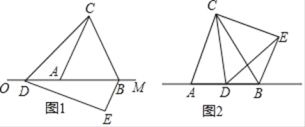
【题目】已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.
(1)如图1,求证:△CDE是等边三角形.
(2)设OD=t,
①当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
②求t为何值时,△DEB是直角三角形(直接写出结果即可).
【答案】(1)见解析;(2) ①见解析; ②t=2或14.
【解析】
(1)由旋转的性质得到∠DCE=60°,DC=EC,即可得到结论;
(2)①当6<t<10时,由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论;
②存在,当点D与点B重合时,D,B,E不能构成三角形;当0≤t<6时,由旋转的性质得到∠ABE=60°,∠BDE<60°,求得∠BED=90°,根据等边三角形的性质得到∠DEB=60°,求得∠CEB=30°,求得OD=OA-DA=6-4=2=t;当6<t<10时,此时不存在;当t>10时,由旋转的性质得到∠DBE=60°,求得∠BDE>60°,于是得到t=14.
(1)∵将△ACD绕点C逆时针方向旋转60°得到△BCE,
∴∠DCE=60°,DC=EC,
∴△CDE是等边三角形;
(2)①存在,当6<t<10时,
由旋转的性质得,BE=AD,
∴C△DBE=BE+DB+DE=AB+DE=4+DE,
由(1)知,△CDE是等边三角形,
∴DE=CD,
∴C△DBE=CD+4,
由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,
此时,CD=2![]() ,
,
∴△BDE的最小周长=CD+4=2![]() +4;
+4;
②存在,∵当点D与点B重合时,D,B,E不能构成三角形,
∴当点D与点B重合时,不符合题意;
当0≤t<6时,由旋转可知,∠ABE=60°,∠BDE<60°,
∴∠BED=90°,
由(1)可知,△CDE是等边三角形,
∴∠DEB=60°,
∴∠CEB=30°,
∵∠CEB=∠CDA,
∴∠CDA=30°,
∵∠CAB=60°,
∴∠ACD=∠ADC=30°,
∴DA=CA=4,
∴OD=OA﹣DA=6﹣4=2,
∴t=2;
当6<t<10时,由∠DBE=120°>90°,
∴此时不存在;
当t>10时,由旋转的性质可知,∠DBE=60°,
又由(1)知∠CDE=60°,
∴∠BDE=∠CDE+∠BDC=60°+∠BDC,
而∠BDC>0°,
∴∠BDE>60°,
∴只能∠BDE=90°,
从而∠BCD=30°,
∴BD=BC=4,
∴OD=14,
∴t=14,
综上所述:当t=2或14时,以D、E、B为顶点的三角形是直角三角形.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
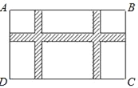
【题目】如图,某小区规划在长20米,宽10米的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AD平行,一条与AB平行,其余部分种草,若使草坪的面积为162米2,问小路应为多宽?
查看答案和解析>>
科目:初中数学 来源: 题型:
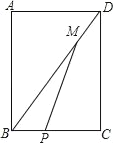
【题目】如图所示,矩形ABCD中,AB=8,BC=6,P是线段BC上一点(P不与B重合),M是DB上一点,且BP=DM,设BP=x,△MBP的面积为y,则y与x之间的函数关系式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
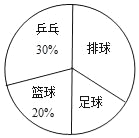
【题目】某校为了调查八年级学生参加“乒乓”、“篮球”、“足球”、“排球”四项体育活动的人数,学校从八年级随机抽取了部分学生进行调查,根据调查结果制作了如下不完整的统计表、统计图:
类别 | 频数(人数) | 频率 |
乒乓 | a | 0.3 |
篮球 | 20 | |
足球 | 15 | b |
排球 | ||
合计 | c | 1 |
请你根据以上信息解答下列各题:
(1)a= ;b= ;c= ;
(2)在扇形统计图中,排球所对应的圆心角是 度;
(3)若该校八年级共有600名学生,试估计该校八年级喜欢足球的人数?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)求扇形统计图中C所对圆心角的度数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:梯形ABCD中,AD//BC,AB⊥BC,AD=3,AB=6,DF⊥DC分别交射线AB、射线CB于点E、F.
(1)当点E为边AB的中点时(如图1),求BC的长;
(2)当点E在边AB上时(如图2),联结CE,试问:∠DCE的大小是否确定?若确定,请求出∠DCE的正切值;若不确定,则设AE=x,∠DCE的正切值为y,请求出y关于x的函数解析式,并写出定义域;
(3)当△AEF的面积为3时,求△DCE的面积.
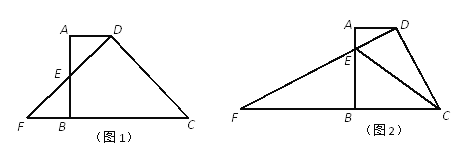
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM∥x轴(如图所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,连接OD.
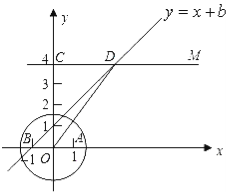
(1)求b的值和点D的坐标;
(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;
(3)在(2)的条件下,如果以PD为半径的圆P与圆O外切,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
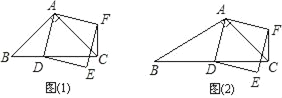
【题目】在△ABC中,∠ACB=45°.点D(与点B、C不重合)为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC.如图①,且点D在线段BC上运动.试判断线段CF与BD之间的位置关系,并证明你的结论.
(2)如果AB≠AC,如图②,且点D在线段BC上运动.(1)中结论是否成立,为什么?
(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P,设AC=4![]() ,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
,BC=3,CD=x,求线段CP的长.(用含x的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com