
【题目】已知:梯形ABCD中,AD//BC,AB⊥BC,AD=3,AB=6,DF⊥DC分别交射线AB、射线CB于点E、F.
(1)当点E为边AB的中点时(如图1),求BC的长;
(2)当点E在边AB上时(如图2),联结CE,试问:∠DCE的大小是否确定?若确定,请求出∠DCE的正切值;若不确定,则设AE=x,∠DCE的正切值为y,请求出y关于x的函数解析式,并写出定义域;
(3)当△AEF的面积为3时,求△DCE的面积.
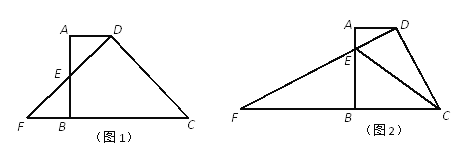
【答案】(1)9;(2)∠DCE的大小确定,![]() .(3)当△AEF的面积为3时,△DCE的面积为25或73.
.(3)当△AEF的面积为3时,△DCE的面积为25或73.
【解析】
(1)根据AD//BC和 E为AB中点,得出 AD= BF,DE= EF,再根据AD=3,AB=6,求出BF=3,再求出DF的值,最后求出CF即可;
(2)作CH⊥AD交AD的延长线于点H,再得出△AED∽△HDC再根据AB⊥AD,CH⊥AD,AD//BC,得出CH =AB=6,然后得出∠DCE的正切值;
(3)当点E在边AB上,设AE=x,根据△AEF的面积为3得出x的值,再求出DE,DC的值,然后可以得出△DCE的面积;当点E在边AB延长线上,设AE=y,根据△AEF的面积为3,得出![]() ,联结CE,作CH⊥AD交AD的延长线于点H,得出DC,DE的值即可.
,联结CE,作CH⊥AD交AD的延长线于点H,得出DC,DE的值即可.
解:(1)∵AD//BC,∴![]() .∵E为AB中点,∴AE=BE. ∴AD= BF,DE= EF.
.∵E为AB中点,∴AE=BE. ∴AD= BF,DE= EF.
∵AD=3,AB=6,∴BF=3,BE=3. ∴BF=BE.
∵AB⊥BC,∴∠F=45°且EF=![]() .
.
∴DF=2EF=![]() .
.
∵DF⊥DC,∠F=45°,∴CF=12.
∴BC= ![]() .
.
(2)∠DCE的大小确定,![]() .
.
作CH⊥AD交AD的延长线于点H,∴∠HCD+∠HDC=90°.
∵DF⊥DC,∴∠ADE+∠HDC=90°. ∴∠HCD=∠ADE.
又∵AB⊥AD,∴∠A=∠CHD. ∴△AED∽△HDC.
∴![]() .
.
∵AB⊥AD,CH⊥AD,AD//BC,∴CH =AB=6.

∵AD=3,CH=6,∴![]() .即
.即![]() .
.
(3)当点E在边AB上,设AE=x,
∵AD//BC,∴![]() ,即
,即![]() .∴
.∴![]() .
.
∵△AEF的面积为3,∴![]() .
.
∴![]() .
.
∵AD=3,AB⊥AD,∴DE=5. ∵![]() ,∴DC=10.
,∴DC=10.
∵DF⊥DC,∴![]() .
.
当点E在边AB延长线上,设AE=y,
∵AD//BC,∴![]() ,即
,即![]() .∴
.∴![]() .
.
∵△AEF的面积为3,∴![]() .∴
.∴![]() .
.
∵AD=3,AB⊥AD,∴DE=![]() .
.
联结CE,作CH⊥AD交AD的延长线于点H,同(1)可得![]() .
.
∴DC=![]()
∵DF⊥DC,∴![]() .
.
综上,当△AEF的面积为3时,△DCE的面积为25或73.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,模块①由15个棱长为1的小正方体构成,模块②-⑥均由4个棱长为1的小正方体构成.现在从模块②-⑥中选出三个模块放到模块①上,与模块①组成一个棱长为![]() 的大正方体.下列四个方案中,符合上述要求的是( )
的大正方体.下列四个方案中,符合上述要求的是( )

A. 模块②,④,⑤ B. 模块③,④,⑥ C. 模块②,⑤,⑥ D. 模块③,⑤,⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
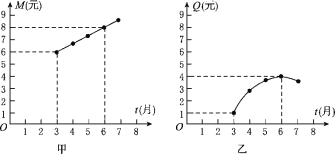
【题目】某公司为指导某种应季商品的生产和销售,对三月份至七月份该商品的售价和成本进行了调研,结果如下:一件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图甲),一件商品的成本Q(元)与时间t(月)的关系可用一段抛物线上的点来表示,其中6月份成本最高(如图乙).根据图象提供的信息解答下面的问题:
(1)一件商品在3月份出售时的利润是多少元?(利润=售价-成本)
(2)求出一件商品的成本Q(元)与时间t(月)之间的函数关系式;
(3)你能求出3月份至7月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗?若该公司能在一个月内售出此种商品30 000件,请你计算该公司在一个月内最少获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
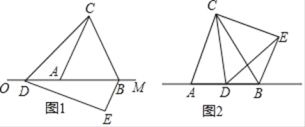
【题目】已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.
(1)如图1,求证:△CDE是等边三角形.
(2)设OD=t,
①当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
②求t为何值时,△DEB是直角三角形(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
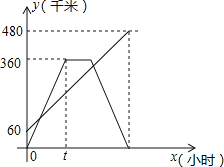
【题目】甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,t= 小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角板![]() 放在平面直角坐标系中,直角边
放在平面直角坐标系中,直角边![]() 垂直
垂直![]() 轴,垂足为
轴,垂足为![]() ,已知
,已知![]() ,点
,点![]() ,
,![]() ,
,![]() 均在反比例函数
均在反比例函数![]() 的图象上,分别作
的图象上,分别作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,且点
,且点![]() 为
为![]() 的中点.
的中点.

![]() 求点
求点![]() 的坐标;
的坐标;
![]() 求四边形
求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上一条运动的线段(点
上一条运动的线段(点![]() 不与点
不与点![]() 重合,点
重合,点![]() 不与点
不与点![]() 重合),且
重合),且![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,在
,在![]() 从左至右的运动过程中,设BM=x,
从左至右的运动过程中,设BM=x,![]() 的面积减去
的面积减去![]() 的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是
的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是
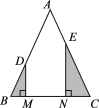
A.  B.
B. 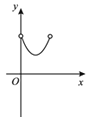 C.
C. 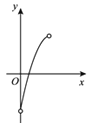 D.
D. 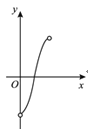
查看答案和解析>>
科目:初中数学 来源: 题型:
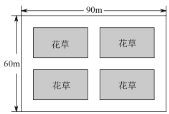
【题目】成都市中心城区“小游园,微绿地”规划已经实施,武侯区某街道有一块矩形空地进入规划试点.如图,已知该矩形空地长为![]() ,宽为
,宽为![]() ,按照规划将预留总面积为
,按照规划将预留总面积为![]() 的四个小矩形区域(阴影部分)种植花草,并在花草周围修建三条横向通道和三条纵向通道,各通道的宽度相等.
的四个小矩形区域(阴影部分)种植花草,并在花草周围修建三条横向通道和三条纵向通道,各通道的宽度相等.
(1)求各通道的宽度;
(2)现有一工程队承接了对这![]() 的区域(阴影部分)进行种植花草的绿化任务,该工程队先按照原计划进行施工,在完成了
的区域(阴影部分)进行种植花草的绿化任务,该工程队先按照原计划进行施工,在完成了![]() 的绿化任务后,将工作效率提高
的绿化任务后,将工作效率提高![]() ,结果提前
,结果提前![]() 天完成任务,求该工程队原计划每天完成多少平方米的绿化任务?
天完成任务,求该工程队原计划每天完成多少平方米的绿化任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com