【题目】如图, CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,∠CEF=60°,则∠ACB=______.
【答案】50°
【解析】
由题意推出∠DCB=∠ABC=70°，结合∠CBF=20°，推出∠CBF=50°，即可推出EF∥AB，EF∥CD，既而推出∠ECD=110°，根据∠DCB=70°，即可推出∠ACB的度数．
解：∵CD∥AB，∠DCB=70°，
∴∠DCB=∠ABC=70°，
∵∠CBF=20°，
∴∠ABF=∠ABC-∠CBF=50°，
∵∠EFB=130°，
∴∠ABF+∠EFB=50°+130°=180°，
∴EF∥AB；
又∵CD∥AB，
∴EF∥CD，
∵∠CEF=60°，
∴∠ECD=120°，
∵∠DCB=70°，
∴∠ACB=∠ECD-∠DCB，
∴∠ACB=50°．
故答案为：50°．
科目：初中数学 来源： 题型：
【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的俯角为α其中tanα=2 
，无人机的飞行高度AH为500 米，桥的长度为1255米．
①求点H到桥左端点P的距离；
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°，求这架无人机的长度AB．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据： 
≈1.414， 
≈1.732）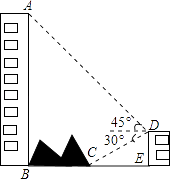
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某山区有23名中、小学生因贫困失学需要捐助，资助一名中学生的学习费用需要a元，一名小学生的学习费用需要b元，某校学生积极捐款，我校初中学生每个年级各自分别捐助的贫困中学生和小学生的人数情况如下表：
（1）求a,b的值.
（2）九年级学生的捐款解决了其余贫困中小学生的学习费用，求九年级学生可捐助的贫困生中、小学生人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：至少有一组对边相等的四边形为“等对边四边形”．
（1）请写出一个你学过的特殊四边形中是“等对边四边形”的名称；
（2）如图1，四边形ABCD是“等对边四边形”，其中AB=CD，边BA与CD的延长线交于点M，点E、F是对角线AC、BD的中点，若∠M=60°，求证：EF
AB；
（3）如图2．在△ABC中，点D、E分别在边AC、AB上，且满足∠DBC=∠ECB∠A，线段CE、BD交于点．
①求证：∠BDC=∠AEC；
②请在图中找到一个“等对边四边形”，并给出证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
中， 
，
；
是向右平移5个单位向上平移4个单位之后得到的图象
（1）
两点的坐标分别为
.
（2）作出平移之后的图形.
（3）求△ABC的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，已知P（1，1）.过点P分别向x轴和y轴作垂线，垂足分别为A，B.
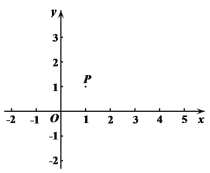
（1）点Q在直线AP上且与点P 的距离为2，则点Q的坐标为 ，三角形BPQ的面积是______；
（2）平移三角形ABP，若顶点P平移后的对应点为
（4，3），
①画出平移后的三角形
；
②直接写出四边形
的面积为 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，点O为对角线AC的中点，过O点的射线OM，ON分别交AB，BC于点E，F，且∠EOF=90°，BO，EF交于点P，则下面结论：
①图形中全等的三角形只有三对；②△EOF是等腰直角三角形；③正方形ABCD的面积等于四边形OEBF面积的4倍；④BE＋BF=
OA．
其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小明同学在点P处测得教学楼A位于北偏东60°方向，办公楼B位于南偏东45°方向．小明沿正东方向前进60米到达C处，此时测得教学楼A恰好位于正北方向．办公楼B正好位于正南方向．求教学楼A与办公楼B之间的距离 ． 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com