
【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的俯角为α其中tanα=2 ![]() ,无人机的飞行高度AH为500
,无人机的飞行高度AH为500 ![]() 米,桥的长度为1255米.
米,桥的长度为1255米.
①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.
【答案】解:①在Rt△AHP中,∵AH=500 ![]() ,
,
由tan∠APH=tanα= ![]() =
= ![]() =2
=2 ![]() ,可得PH=250米.
,可得PH=250米.
∴点H到桥左端点P的距离为250米.
②设BC⊥HQ于C.
在Rt△BCQ中,∵BC=AH=500 ![]() ,∠BQC=30°,
,∠BQC=30°,
∴CQ= ![]() =1500米,
=1500米,
∵PQ=1255米,
∴CP=245米,
∵HP=250米,
∴AB=HC=250﹣245=5米.
答:这架无人机的长度AB为5米.
【解析】①在Rt△AHP中,由tan∠APH=tanα= ![]() ,即可解决问题;②设BC⊥HQ于C.在Rt△BCQ中,求出CQ=
,即可解决问题;②设BC⊥HQ于C.在Rt△BCQ中,求出CQ= ![]() =1500米,由PQ=1255米,可得CP=245米,再根据AB=HC=PH﹣PC计算即可;
=1500米,由PQ=1255米,可得CP=245米,再根据AB=HC=PH﹣PC计算即可;
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】某家电集团公司研制生产的新家电,前期投资 ![]() 万元,每生产一台这种新家电,后期还需其他投资
万元,每生产一台这种新家电,后期还需其他投资![]() 万元,已知每台新家电售价为
万元,已知每台新家电售价为 ![]() 万元,设总投资为
万元,设总投资为![]() 万元(总投资
万元(总投资![]() 前期投资
前期投资![]() 后期投资),总利润为
后期投资),总利润为![]() 万元(总利润
万元(总利润![]() 总售价
总售价![]() 总投资),新家电总产量为
总投资),新家电总产量为![]() 台,(假设可按产量全部卖出)
台,(假设可按产量全部卖出)
(1)试用含![]() 的代数式表示
的代数式表示![]() 和
和![]() ;
;
(2)问新家电总产量超过多少台时,该公司开始盈利?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠BAC=40°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为____________.
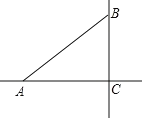
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园内有一个花坛,是由两个边长均为2.5m的正六边形围成的(如图中的阴影部分所示),学校现要将这个花坛在原有的基础上扩建成一个如图所示的菱形区域,则扩建后菱形区域的周长为( )

A.30mB.![]() mC.20mD.
mC.20mD.![]() m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABO中,A(﹣2,﹣3)、B(2,﹣1),三角形A′B′O′是三角形ABO平移之后得到的图形,并且O的对应点O′的坐标为(4,3).
(1)求三角形ABO的面积;
(2)作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′ 、B′ ;
(3)P(x,y)为三角形ABO中任意一点,则平移后对应点P′的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式.
例如:化简![]() .
.
解:将分子、分母同乘以![]() 得:
得:![]() .
.
类比应用:
(1)化简:![]() ;
;
(2)化简:![]() .
.
拓展延伸:
宽与长的比是![]() 的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
(1)黄金矩形ABCD的长BC= ;
(2)如图②,将图①中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论;

(3)在图②中,连结AE,则点D到线段AE的距离为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的方程![]() ,
,
(1)求证:无论k取任何实数值,方程总有实数根;
(2)若等腰三角形ABC的一边长a=1,两个边长b,c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈ ![]() ,tan48°≈
,tan48°≈ ![]() ,sin64°≈
,sin64°≈ ![]() ,tan64°≈2)
,tan64°≈2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com