
【题目】定义:至少有一组对边相等的四边形为“等对边四边形”.

(1)请写出一个你学过的特殊四边形中是“等对边四边形”的名称;
(2)如图1,四边形ABCD是“等对边四边形”,其中AB=CD,边BA与CD的延长线交于点M,点E、F是对角线AC、BD的中点,若∠M=60°,求证:EF![]() AB;
AB;
(3)如图2.在△ABC中,点D、E分别在边AC、AB上,且满足∠DBC=∠ECB![]() ∠A,线段CE、BD交于点.
∠A,线段CE、BD交于点.
①求证:∠BDC=∠AEC;
②请在图中找到一个“等对边四边形”,并给出证明.
【答案】(1)如:平行四边形、矩形、菱形、等腰梯形等;(2)证明见解析;(3)①证明见解析;②四边形EBCD是等对边四边形.证明见解析.
【解析】
(1)理解等对边四边形的图形的定义,有平行四边形、矩形、菱形、等腰梯形等,可得出答案.
(2)取BC的中点N,连结EN,FN,由中位线定理可得EN=12CD,FN=12AB,可证明△EFN为等边三角形,则结论得证;
(3)①证明∠EOB=∠A,利用四边形内角和可证明∠BDC=∠AEC;
②作CG⊥BD于G点,作BF⊥CE交CE延长线于F点.根据AAS可证明△BCF≌△CBG,则BF=CG,证明△BEF≌△CDG,可得BE=CD,则四边形EBCD是“等对边四边形”.
(1)如:平行四边形、矩形、菱形、等腰梯形等.
(2)如图1,取BC的中点N,连结EN,FN,
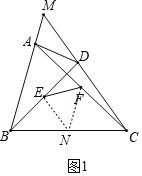
∴EN![]() CD,FN
CD,FN![]() AB,
AB,
∴EN=FN.
∵∠M=60°,
∴∠MBC+∠MCB=120°.
∵FN∥AB,EN∥MC,
∴∠FNC=∠MBC,∠ENB=∠MCB,
∴∠ENF=180°﹣120°=60°,
∴△EFN为等边三角形,
∴EF=FN![]() AB.
AB.
(3)①证明:∵∠BOE=∠BCE+∠DBC,∠DBC=∠ECB![]() ∠A,
∠A,
∴∠BOE=2∠DBC=∠A.
∵∠A+∠AEC+∠ADB+∠EOD=360°,∠BOE+∠EOD=180°,
∴∠AEC+∠ADB=180°.
∵∠ADB+∠BDC=180°,
∴∠BDC=∠AEC;
②解:此时存在等对边四边形,是四边形EBCD.
如图2,作CG⊥BD于G点,作BF⊥CE交CE延长线于F点.
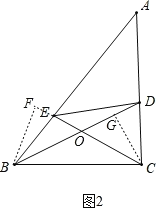
∵∠DBC=∠ECB![]() ∠A,BC=CB,∠BFC=∠BGC=90°,
∠A,BC=CB,∠BFC=∠BGC=90°,
∴△BCF≌△CBG(AAS),
∴BF=CG.
∵∠BEF=∠ABD+∠DBC+∠ECB,∠BDC=∠ABD+∠A,
∴∠BEF=∠BDC,
∴△BEF≌△CDG(AAS),
∴BE=CD,
∴四边形EBCD是等对边四边形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,三角形ABO中,A(﹣2,﹣3)、B(2,﹣1),三角形A′B′O′是三角形ABO平移之后得到的图形,并且O的对应点O′的坐标为(4,3).
(1)求三角形ABO的面积;
(2)作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′ 、B′ ;
(3)P(x,y)为三角形ABO中任意一点,则平移后对应点P′的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6 ![]() 米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.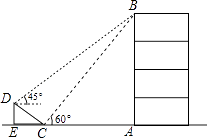
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示:

根据以上信息,请解答下面的问题;
选手 | A平均数 | 中位数 | 众数 | 方差 |
甲 | a | 8 | 8 | c |
乙 | 7.5 | b | 6和9 | 2.65 |
(1)补全甲选手10次成绩频数分布图.
(2)a= ,b= ,c= .
(3)教练根据两名选手手的10次成绩,决定选甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.(tan31°≈0.6,tan50°≈1.2,结果精确到1m)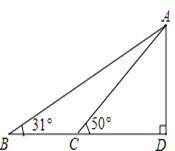
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )

A.3
B.4
C.1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某城市的电视塔AB坐落在湖边,数学老师带领学生隔湖测量电视塔AB的高度,在点M处测得塔尖点A的仰角∠AMB为22.5°,沿射线MB方向前进200米到达湖边点N处,测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°,则电视塔AB的高度为米(结果保留根号).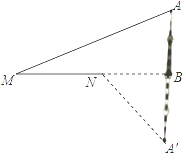
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com