
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.(tan31°≈0.6,tan50°≈1.2,结果精确到1m)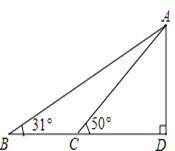
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
【答案】
(1)解:在Rt△ABD中,
∵AD=24m,∠B=31°,
∴tan31°= ![]() ,
,
即BD= ![]() =40m,
=40m,
在Rt△ACD中,
∵AD=24m,∠ACD=50°,
∴tan50°= ![]() ,
,
即CD= ![]() =20m,
=20m,
∴BC=BD﹣CD=40﹣20=20m,
即B,C的距离为20m.
(2)解:根据题意得:
20÷2=10m/s<15m/s,
即此轿车没有超速.
【解析】(1)在Rt△ABD中,根据锐角三角函数定义可得BD=AD·tan31°=40m,在Rt△ACD中,根据锐角三角函数定义可得CD=AD·tan50°=20m,再由BC=BD﹣CD即可得出B,C的距离.
(2)根据速度=路程÷时间,再与15m/s比较即可得出此轿车有没有超速.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8, ![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求: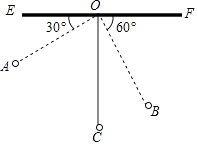
(1)单摆的长度( ![]() ≈1.7);
≈1.7);
(2)从点A摆动到点B经过的路径长(π≈3.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:至少有一组对边相等的四边形为“等对边四边形”.

(1)请写出一个你学过的特殊四边形中是“等对边四边形”的名称;
(2)如图1,四边形ABCD是“等对边四边形”,其中AB=CD,边BA与CD的延长线交于点M,点E、F是对角线AC、BD的中点,若∠M=60°,求证:EF![]() AB;
AB;
(3)如图2.在△ABC中,点D、E分别在边AC、AB上,且满足∠DBC=∠ECB![]() ∠A,线段CE、BD交于点.
∠A,线段CE、BD交于点.
①求证:∠BDC=∠AEC;
②请在图中找到一个“等对边四边形”,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,3),B(3,0),C(3,4)三点,点P(x,﹣0.5x),当△ABP的面积等于△ABC的面积时,则P点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知P(1,1).过点P分别向x轴和y轴作垂线,垂足分别为A,B.
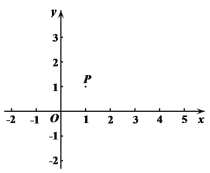
(1)点Q在直线AP上且与点P 的距离为2,则点Q的坐标为 ,三角形BPQ的面积是______;
(2)平移三角形ABP,若顶点P平移后的对应点为![]() (4,3),
(4,3),
①画出平移后的三角形![]() ;
;
②直接写出四边形![]() 的面积为 .
的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
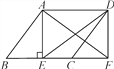
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2

(1)求证:△ABC≌△ADE;
(2)找出图中与∠1、∠2相等的角(直接写出结论,不需证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com