
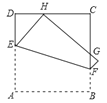
【题目】如图,将正方形ABCD折叠,使点A与CD边上的点H重合(H不与C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD周长为m,△CHG周长为n,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由题意连接AH、AG,作AM⊥HG于M.利用正方形的性质以及全等三角形的判定与性质进行等量替换从而求出![]() 的值.
的值.
解:连接AH、AG,作AM⊥HG于M.
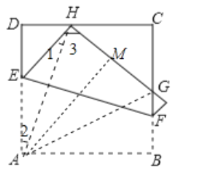
∵四边形ABCD是正方形,
∴AD=AB.
∴AM=AB.
∵EA=EH,
∴∠1=∠2,
∵∠EAB=∠EHG=90°,
∴∠HAB=∠AHG,
∵DH∥AB,
∴∠DHA=∠HAB=∠AHM,
∵AH=AH,∠D=∠AMH=90°,
∴△AHD≌△AHM,
∴DH=HM,AD=AM,
∵AM=AB,AG=AG,
∴Rt△AGM≌Rt△AGB,
∴GM=GB,
∴△GCH的周长=n=CH+HM+MG+CG=CH+DH+CG+GB=2BC,
∵四边形ABCD的周长=m=4BC,
∴![]() .
.
故选:B.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)试用树状图或列表法中的一种列举出这两中的一种列举出这辆汽车行驶方向所有可能的结果;
(2)求至少有一辆汽车向左转的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司拟用运营指数y来量化考核司机的工作业绩,运营指数(y)与运输次数(n)和平均速度(x)之间满足关系式为y=ax2+bnx+100,当n=1,x=30时,y=190;当n=2,x=40时,y=420
用含x和n的式子表示y;
当运输次数定为3次,求获得最大运营指数时的平均速度;
若n=2,x=40,能否在n增加m%(m>0),同时x减少m%的情况下,而y的值保持不变,若能,求出m的值;若不能,请说明理由.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
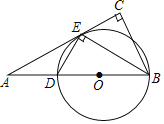
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点P是CD上一动点,连结PA,分别过点B、D作BE⊥PA、DF⊥PA,垂足为E、F,如图①.
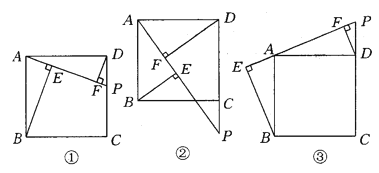
(1)请探索BE、DF、EF这三条线段长度具有怎样的数量关系,若点P在DC的延长线上(如图②),那么这三条线段的长度之间又有怎样的数量关系?若点P在CD的延长线上呢(如图③)?请分别直接写出结论.
(2)请在(1)中的三个结论中选择一个加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件![]() 元,出厂价为每件
元,出厂价为每件![]() 元,每月销售量
元,每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:![]() .
.
(1)李明在开始创业的第一个月将销售单价定为![]() 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为![]() (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于![]() 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于![]() 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市以20元/千克的进货价购进了一批绿色食品,如果以30元/千克销售这些绿色食品,那么每天可售出400千克.由销售经验可知,每天的销售量y(千克)与销售单价x(元)(x≥30)存在如图所示的一次函数关系.
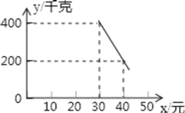
(1)试求出y与x的函数关系式;
(2)设该超市销售该绿色食品每天获得利润w元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李准备进行如下的操作,把一根长![]() 的铁丝剪成两段,并把每段首尾相连各围成一个长宽不等的矩形,两矩形相似且相似比为
的铁丝剪成两段,并把每段首尾相连各围成一个长宽不等的矩形,两矩形相似且相似比为![]() .
.
(1)要使这两个矩形的面积之和为![]() ,较小矩形的长宽各是多少?
,较小矩形的长宽各是多少?
(2)小李认为这两个矩形的面积和不可能为![]() ,你同意吗?说明理由.(说明:相似多边形的周长比等于相似比,面积比等于相似比的平方)
,你同意吗?说明理由.(说明:相似多边形的周长比等于相似比,面积比等于相似比的平方)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在y轴,x轴上,点B的坐标为![]() ,直线
,直线![]() 分别交AB,BC于点M,N,
分别交AB,BC于点M,N,![]() ,反比例函数
,反比例函数![]() 图象经过点M,N.
图象经过点M,N.
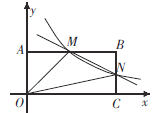
(1)求反比例函数的表达式;
(2)根据图象,请直接写出不等式![]() 的解集________.
的解集________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com