
【题目】如图,△ABC内接于⊙O,∠B=600,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
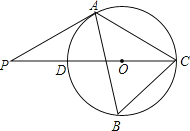
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.
【答案】(1)见解析(2)2![]()
【解析】解:(1)证明:连接OA,
∵∠B=600,∴∠AOC=2∠B=1200。
∵OA=OC,∴∠OAC=∠OCA=300。
又∵AP=AC,∴∠P=∠ACP=300。
∴∠OAP=∠AOC﹣∠P=900。∴OA⊥PA。
∵OA是⊙O的半径,∴PA是⊙O的切线。
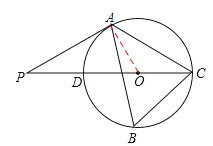
(2)在Rt△OAP中,∵∠P=300,
∴PO=2OA=OD+PD。
又∵OA=OD,∴PD=OA。
∵PD=![]() ,∴2OA=2PD=2
,∴2OA=2PD=2![]() 。
。
∴⊙O的直径为2![]() 。.
。.
(1)连接OA,根据圆周角定理求出∠AOC,再由OA=OC得出∠ACO=∠OAC=300,再由AP=AC得出
∠P=300,继而由∠OAP=∠AOC﹣∠P,可得出OA⊥PA,从而得出结论。
(2)利用含300的直角三角形的性质求出OP=2OA,可得出OP﹣PD=OD,再由PD=![]() ,可得出⊙O的直径。
,可得出⊙O的直径。


科目:初中数学 来源: 题型:
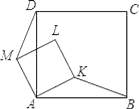
【题目】如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品,甲种商品的进价比乙种商品的进价每件多80元,若用720元购进甲种商品的件数与用360元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价各是多少元?
(2)已知甲种商品的售价为240元/件,乙种商品的售价为130元/件,若超市销售甲、乙两种商品共80件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完80件甲、乙两种商品的总利润为
),设销售完80件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.
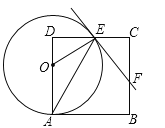
(1)求证:△ODE∽△ECF;
(2)在点O的运动过程中,设DE= ![]() :
:
①求![]() 的最大值,并求此时⊙O的半径长;
的最大值,并求此时⊙O的半径长;
②判断△CEF的周长是否为定值,若是,求出△CEF的周长;否则,请说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
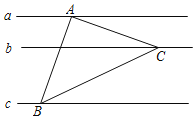
【题目】在同一平面内,有相互平行的三条直线a,b,c,且a,b之间的距离为1,b,c之间的距离是2,若等腰Rt△ABC的三个顶点恰好各在这三条平行直线上,如图所示,则△ABC的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识背景)我国古代把直角三角形较短的直角边称为“勾”,较长的的直角边称为“股”,斜边称为“弦”.据《周髀算经》记载,公元前1000多年就发现了“勾三股四弦五”的结论.像3、4、5这样为三边长能构成直角三角形的3个正整数,称为勾股数.
(应用举例)
观察3,4,5;5,12,13;7,24,25;![]()
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,
当勾为3时,股![]() ,弦
,弦![]() ;
;
当勾为5时,股![]() ,弦
,弦![]() ;
;
当勾为7时,股![]() ,弦
,弦![]() .
.
请仿照上面三组样例,用发现的规律填空:
(1)如果勾用![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股
的式子表示股和弦,则股![]() ,弦
,弦![]() .
.
(问题解决)
(2)古希腊的哲学家柏拉图也提出了构造勾股数组的公式.具体表述如下:如果![]() ,
,![]() ,
,![]() 为大于1的整数),则
为大于1的整数),则![]() 、
、![]() 、
、![]() 为勾股数.请你证明柏拉图公式的正确性;
为勾股数.请你证明柏拉图公式的正确性;
(3)毕达哥拉斯在他找到的勾股数的表达式中发现弦与股的差为1,若用![]() 为任意正整数)表示勾股数中最大的一个数,请你找出另外两个数的表达式分别是多少.
为任意正整数)表示勾股数中最大的一个数,请你找出另外两个数的表达式分别是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=∠C,点D在AC上,点E在BC上,AD=CE,BC=DC
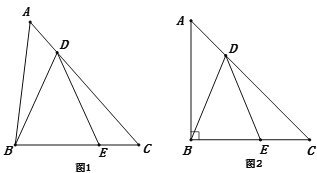
(1)求证:DB=DE;
(2)如图2,若∠ABC=90°,求∠BED的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC,任取一点O,连接AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法:①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF的周长比为1∶2;④△ABC与△DEF的面积比为4∶1. 正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com