
ЎҫМвДҝЎҝИзНјКЗёщҫЭ¶ФДіЗшіхЦРИэёцДкј¶С§ЙъҝОНвФД¶БөДЎ°Вю»ӯҙФКйЎұЎўЎ°ҝЖЖХіЈК¶ЎұЎўЎ°ГыИЛҙ«јЗЎұЎўЎ°ЖдЛьЎұЦРЈ¬ЧоПІ»¶ФД¶БөДТ»ЦЦ¶БОпҪшРРЛж»ъійСщөчІйЈ¬Іў»жЦЖБЛПВГжІ»НкХыөДМхРОНіјЖНјәНЙИРОНіјЖНјЈЁГҝИЛұШСЎТ»ЦЦ¶БОпЈ¬ІўЗТЦ»ДЬСЎТ»ЦЦЈ©Ј¬ёщҫЭМṩөДРЕПўЈ¬ҪвҙрПВБРОКМвЈә
ЈЁ1Ј©ЗуёГЗшійСщөчІйИЛКэЈ»
ЈЁ2Ј©І№И«МхРОНіјЖНјЈ¬ІўЗуіцЧоПІ»¶Ў°ЖдЛьЎұ¶БОпөДИЛКэФЪЙИРОНіјЖНјЦРЛщХјөДФІРДҪЗ¶ИКэЈ»
ЈЁ3Ј©ИфёГЗшУРіхЦРЙъ14400ИЛЈ¬№АјЖёГЗшУРіхЦРЙъЧоПІ»¶¶БЎ°ГыИЛҙ«јЗЎұөДС§ЙъКЗ¶аЙЩИЛЈҝ
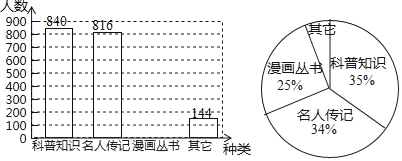
Ўҫҙр°ёЎҝЈЁ1Ј©ёГЗшійСщөчІйөДИЛКэКЗ2400ИЛЈ»ЈЁ2Ј©јыҪвОцЈ¬ЧоПІ»¶Ў°ЖдЛьЎұ¶БОпөДИЛКэФЪЙИРОНіјЖНјЦРЛщХјөДФІРДҪЗКЗ¶ИКэ21.6ЎгЈ»ЈЁ3Ј©№АјЖЧоПІ»¶¶БЎ°ГыИЛҙ«јЗЎұөДС§ЙъКЗ4896ИЛ
ЎҫҪвОцЎҝ
ЈЁ1Ј©УЙЎ°ҝЖЖХЦӘК¶ЎұИЛКэј°Жд°Щ·ЦұИҝЙөГЧЬИЛКэЈ»
ЈЁ2Ј©ЧЬИЛКэіЛТФЎ°Вю»ӯҙФКйЎұөДИЛКэЗуөГЖдИЛКэјҙҝЙІ№И«НјРОЈ¬УГ360ЎгіЛТФЎ°ЖдЛыЎұИЛКэЛщХјұИАэҝЙөГЈ»
ЈЁ3Ј©ЧЬИЛКэіЛТФЎ°ГыИЛҙ«јЗЎұөД°Щ·ЦұИҝЙөГЈ®
ЈЁ1Ј©840ЎВ35%=2400ЈЁИЛЈ©Ј¬
ЎаёГЗшійСщөчІйөДИЛКэКЗ2400ИЛЈ»
ЈЁ2Ј©2400ЎБ25%=600ЈЁИЛЈ©Ј¬
ЎаёГЗшійСщөчІйЧоПІ»¶Ў°Вю»ӯҙФКйЎұөДИЛКэКЗ600ИЛЈ¬
І№И«НјРОИзПВЈә
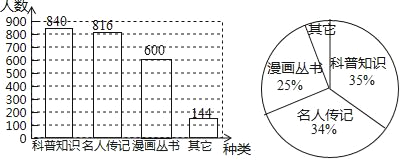
![]() ЎБ360Ўг=21.6ЎгЈ¬
ЎБ360Ўг=21.6ЎгЈ¬
ЎаЧоПІ»¶Ў°ЖдЛьЎұ¶БОпөДИЛКэФЪЙИРОНіјЖНјЦРЛщХјөДФІРДҪЗКЗ¶ИКэ21.6ЎгЈ»
ЈЁ3Ј©ҙУСщұҫ№АјЖЧЬМеЈә14400ЎБ34%=4896ЈЁИЛЈ©Ј¬
ҙрЈә№АјЖЧоПІ»¶¶БЎ°ГыИЛҙ«јЗЎұөДС§ЙъКЗ4896ИЛЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
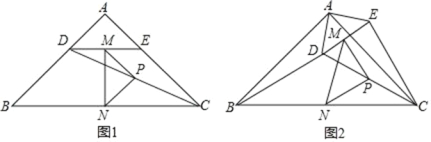
ЎҫМвДҝЎҝИзНј 1Ј¬ФЪ RtЎчABC ЦРЈ¬ЎПA=90ЎгЈ¬AB=ACЈ¬өг DЎўE ·ЦұрФЪұЯ ABЎўAC ЙПЈ¬AD=AEЈ¬Б¬ҪУDCЈ¬өг MЎўPЎўN ·ЦұрОӘ DEЎўDCЎўBC өДЦРөг,
(1)№ЫІмІВПлЈәИзНј 1 ЦРЈ¬ЎчPMN КЗ ИэҪЗРОЈ»
(2)МҪҫҝЦӨГчЈә°СЎчADE ИЖөг A ДжКұХл·ҪПтРэЧӘөҪНј 2 өДО»ЦГЈ¬Б¬ҪУ MNЈ¬BDЈ¬ CEЈ®ЕР¶ПЎчPMN өДРОЧҙЈ¬ІўЛөГчАнУЙЈ»
(3)НШХ№СУЙмЈәҪ«ЎчADE ИЖөг A ФЪЖҪГжДЪЧФУЙРэЧӘЈ¬Иф AD=4Ј¬AB=10Ј¬ЗлЗуЎчPMN Гж»эөДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ¶юҙОәҜКэy=ax2+bx+cөДНјПуИзНјЛщКҫЈ¬ПВБРҪбВЫЈәўЩ9a©Ғ3b+c=0Ј»ўЪ4a©Ғ2b+cЈҫ0Ј»ўЫ·ҪіМax2+bx+c©Ғ4=0УРБҪёцПаөИөДКөКэёщЈ»ўЬ·ҪіМaЈЁx©Ғ1Ј©2+bЈЁx©Ғ1Ј©+c=0өДБҪёщКЗx1=©Ғ2Ј¬x2=2Ј®ЖдЦРХэИ·ҪбВЫөДёцКэКЗЈЁЎЎЎЎЈ©

A. 1 B. 2 C. 3 D. 4
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬УРТ»ҝйЦұҪЗИэҪЗРОЦҪЖ¬Ј¬БҪЦұҪЗұЯABЈҪ6Ј¬BCЈҪ8Ј¬Ҫ«ЎчABCХЫөюЈ¬К№ABВдФЪРұұЯACЙПЈ¬ХЫәЫОӘADЈ¬ФтBDөДіӨОӘ(ЎЎ)

A. 6B. 5C. 4D. 3
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
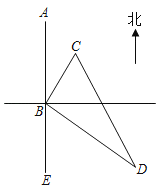
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬РТёЈРЎЗшCО»УЪҝмөЭХҫөгBөДұұЖ«¶«35Ўг·ҪПтЈ¬ЗЯФ·РЎЗшDО»УЪBөДДПЖ«¶«55Ўг·ҪПтЈ¬ОЮИЛ»ъТФ1З§ГЧ/·ЦЦУөДЛЩ¶ИЕдЛНҝмөЭКұЈ¬ҙУBөҪCРи·ЙРР8·ЦЦУЈ¬ҙУBөҪDРи·ЙРР15·ЦЦУЈ®ИфОЮИЛ»ъөДЕдЛНВ·ПЯКЗBЎъCЎъDЎъBЗлЗуіцЕдЛННҫЦР·ЙРРЛщРиКұјдЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
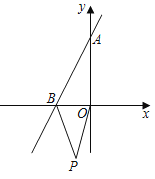
ЎҫМвДҝЎҝИзНјЈ¬ЦұПЯyЈҪ2x+4·ЦұрУлxЦбЈ¬yЦбҪ»УЪBЈ¬AБҪөг
ЈЁ1Ј©ЗуЎчABOөДГж»эЈ»
ЈЁ2Ј©Из№ыФЪөЪИэПуПЮДЪУРТ»өгP(©Ғ1Ј¬m)Ј¬ЗлУГә¬mөДКҪЧУұнКҫЛДұЯРОAOPBөДГж»эЈ»
ЈЁ3Ј©ФЪЈЁ2Ј©өДМхјюПВЈ¬КЗ·сҙжФЪөгPЈ¬К№ЛДұЯРОAOPBөДГж»эКЗЎчABOГж»эөД2ұ¶ЈҝИфҙжФЪЈ¬ЗлЗуіцөгPөДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬ТФAОӘФІРДЈ¬ИОТвіӨОӘ°лҫ¶»ӯ»Ў·ЦұрҪ»ABЎўACУЪөгMәНNФЩ·ЦұрТФMNОӘФІРДЈ¬ҙуУЪ
Ј¬ТФAОӘФІРДЈ¬ИОТвіӨОӘ°лҫ¶»ӯ»Ў·ЦұрҪ»ABЎўACУЪөгMәНNФЩ·ЦұрТФMNОӘФІРДЈ¬ҙуУЪ![]() өДіӨОӘ°лҫ¶»ӯ»ЎЈ¬БҪ»ЎҪ»УЪөгPЈ¬Б¬ҪУAPІўСУіӨҪ»BCУЪөгDЈ¬ФтПВБРЛө·ЁЦРХэИ·өДУР________Ј®
өДіӨОӘ°лҫ¶»ӯ»ЎЈ¬БҪ»ЎҪ»УЪөгPЈ¬Б¬ҪУAPІўСУіӨҪ»BCУЪөгDЈ¬ФтПВБРЛө·ЁЦРХэИ·өДУР________Ј®
ўЩADКЗ![]() өДЖҪ·ЦПЯЈ»ўЪ
өДЖҪ·ЦПЯЈ»ўЪ![]() Ј»ўЫөгDФЪABөДЦРҙ№ПЯЙПЈ»ўЬ
Ј»ўЫөгDФЪABөДЦРҙ№ПЯЙПЈ»ўЬ![]()

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЕЧОпПЯy=x2+bx+cУлxЦбҪ»УЪAЈЁ©Ғ1Ј¬0Ј©әНBЈЁ3Ј¬0Ј©БҪөгЈ¬Ҫ»yЦбУЪөгEЈ®
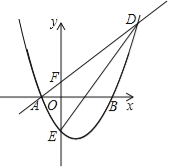
ЈЁ1Ј©ЗуҙЛЕЧОпПЯөДҪвОцКҪЈ®
ЈЁ2Ј©ИфЦұПЯy=x+1УлЕЧОпПЯҪ»УЪAЎўDБҪөгЈ¬УлyЦбҪ»УЪөгFЈ¬Б¬ҪУDEЈ¬ЗуЎчDEFөДГж»эЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘЕЧОпПЯ![]() Ул
Ул![]() ЦбөДТ»ёцҪ»өг
ЦбөДТ»ёцҪ»өг![]() Ј®
Ј®
ЈЁ1Ј©КФ·ЦұрЗуіцХвМхЕЧОпПЯУл![]() ЦбөДБнТ»ёцҪ»өг
ЦбөДБнТ»ёцҪ»өг![]() ј°Ул
ј°Ул![]() ЦбөДҪ»өг
ЦбөДҪ»өг![]() өДЧшұкЈ®
өДЧшұкЈ®
ЈЁ2Ј©ЙиЕЧОпПЯөД¶ҘөгОӘ![]() Ј¬ЗлФЪНјЦР»ӯіцЕЧОпПЯөДІЭНјЈ¬Ифөг
Ј¬ЗлФЪНјЦР»ӯіцЕЧОпПЯөДІЭНјЈ¬Ифөг![]() ФЪЦұПЯ
ФЪЦұПЯ![]() ЙПЈ¬КФЕР¶П
ЙПЈ¬КФЕР¶П![]() өгКЗ·сФЪҫӯ№э
өгКЗ·сФЪҫӯ№э![]() өгөД·ҙұИАэәҜКэөДНјПуЙПЈ¬ІўЛөГчАнУЙЈ»
өгөД·ҙұИАэәҜКэөДНјПуЙПЈ¬ІўЛөГчАнУЙЈ»
ЈЁ3Ј©КФЗу![]() өДЦөЈ®
өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com