
【题目】如图,已知抛物线![]() 与
与![]() 轴的一个交点
轴的一个交点![]() .
.
(1)试分别求出这条抛物线与![]() 轴的另一个交点
轴的另一个交点![]() 及与
及与![]() 轴的交点
轴的交点![]() 的坐标.
的坐标.
(2)设抛物线的顶点为![]() ,请在图中画出抛物线的草图,若点
,请在图中画出抛物线的草图,若点![]() 在直线
在直线![]() 上,试判断
上,试判断![]() 点是否在经过
点是否在经过![]() 点的反比例函数的图象上,并说明理由;
点的反比例函数的图象上,并说明理由;
(3)试求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)把A点的坐标代入抛物线的解析式,就可以求出m的值,得到抛物线的解析式.在解析式中令y=0,解方程就可以求出与x轴的交点;(2)根据函数解析式就可求出抛物线的顶点坐标,利用待定系数法求出反比例函数的解析式.经过C,B的直线解析式可以用待定系数法求得,进而求出E点的坐标.把E的坐标代入反比例函数解析式,就可以判断是否在反比例函数的图象上;(3)过D作DF⊥y轴于点F,则△CFD为等腰直角三角形,△AOC是等腰直角三角形,根据勾股定理就可以求出CD,AC的长度.Rt△ADC中根据三角函数的定义就可以求出三角函数值.
解:(1)因为![]() 在抛物线
在抛物线![]() 上,
上,
则![]() ,解得
,解得![]() .
.
所以抛物线的解析式为![]() .
.
因为![]() 点为抛物线与
点为抛物线与![]() 轴的交点,求得
轴的交点,求得![]() ,
,
因为![]() 点为抛物线与
点为抛物线与![]() 轴的交点,求得
轴的交点,求得![]() .
.
(2)∵![]() ,
,
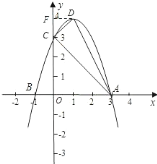
∴顶点![]() ,
,
画这个函数的草图.
由![]() ,
,![]() 点的坐标可求得直线
点的坐标可求得直线![]() 的解析式为
的解析式为![]() ,
,
∵点![]() 在
在![]() 上,
上,
∴![]() .
.
可求得过![]() 点的反比例函数的解析式为
点的反比例函数的解析式为![]() .
.
当![]() 时,
时,![]() .
.
∴点![]() 不在过
不在过![]() 点的反比例函数图象上.
点的反比例函数图象上.
(3)过![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() .
.
连接![]() ,则
,则![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() .
.
因为![]() ,
,
∴![]() 中,
中,![]() .
.
另解:∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
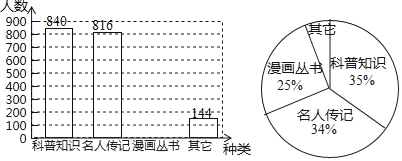
【题目】如图是根据对某区初中三个年级学生课外阅读的“漫画丛书”、“科普常识”、“名人传记”、“其它”中,最喜欢阅读的一种读物进行随机抽样调查,并绘制了下面不完整的条形统计图和扇形统计图(每人必选一种读物,并且只能选一种),根据提供的信息,解答下列问题:
(1)求该区抽样调查人数;
(2)补全条形统计图,并求出最喜欢“其它”读物的人数在扇形统计图中所占的圆心角度数;
(3)若该区有初中生14400人,估计该区有初中生最喜欢读“名人传记”的学生是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() .
.

![]() 如图1,若
如图1,若![]() ,
,![]() ,
,![]() ,且
,且![]() ,求AD的长;
,求AD的长;
![]() 如图2,请利用没有刻度的直尺和圆规,在线段AB上找一点F,使得点F到边AC的距离等于
如图2,请利用没有刻度的直尺和圆规,在线段AB上找一点F,使得点F到边AC的距离等于![]() 注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注
注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于G,交BE于H.下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中所有正确结论的序号是

A.①②③④B.①②③C.②④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
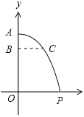
【题目】某地区遭受严重的自然灾害,空军某部队奉命赶灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱航口![]() ,如图所示,如果空投物资离开
,如图所示,如果空投物资离开![]() 处后下落的垂直高度
处后下落的垂直高度![]() 米时,它测
米时,它测![]() 处的水平距离
处的水平距离![]() 米,那么要使飞机在垂直高度
米,那么要使飞机在垂直高度![]() 米的高空进行空投,物资恰好准确地落在居民点
米的高空进行空投,物资恰好准确地落在居民点![]() 处,飞机到
处,飞机到![]() 处的水平距离
处的水平距离![]() 应为________米.
应为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示经过原点,给出以下四个结论:①abc=0,②a+b+c>0,③2a>b,④4ac﹣b2<0;其中正确的结论有( )
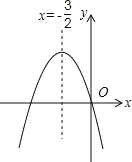
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中说明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),求∠BDG的度数.
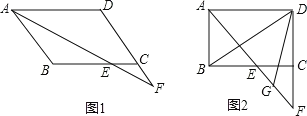
查看答案和解析>>
科目:初中数学 来源: 题型:
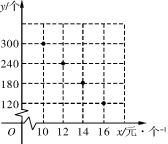
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量![]() (单位:个)与销售单价
(单位:个)与销售单价![]() (单位:元/个)之间的对应关系如图所示:
(单位:元/个)之间的对应关系如图所示:
(1) ![]() 与
与![]() 之间的函数关系是 .
之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润![]() (单位:元)与销售单价
(单位:元)与销售单价![]() (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com