
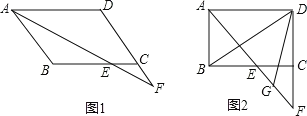
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
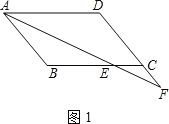
(1)在图1中说明CE=CF;
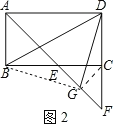
(2)若∠ABC=90°,G是EF的中点(如图2),求∠BDG的度数.
【答案】(1)答案见解析;(2)∠BDG=45°.
【解析】
(1)先根据角平分线的定义可得![]() ,再根据平行四边形的性质、平行线的性质可得
,再根据平行四边形的性质、平行线的性质可得![]() ,从而可得
,从而可得![]() ,然后根据等腰三角形的性质即可得证;
,然后根据等腰三角形的性质即可得证;
(2)先根据矩形的性质和题(1)的结论可得出![]() 为等腰直角三角形,再根据等腰三角形的性质可得
为等腰直角三角形,再根据等腰三角形的性质可得![]() ,然后根据角平分线的定义、等腰三角形的判定与性质可得
,然后根据角平分线的定义、等腰三角形的判定与性质可得![]() ,从而可得
,从而可得![]() ,最后根据三角形全等的判定定理与性质可得
,最后根据三角形全等的判定定理与性质可得![]() ,从而可推出
,从而可推出![]() 为等腰直角三角形,由此即可得出答案.
为等腰直角三角形,由此即可得出答案.
(1)如图1,AF平分![]()
![]()
∵四边形ABCD是平行四边形
![]()
![]()
![]()
![]() ;
;
(2)如图2,连接GC、BG
∵四边形ABCD为平行四边形,![]()
∴四边形ABCD为矩形
![]()
![]()
结合(1)的结论得,![]() 为等腰直角三角形
为等腰直角三角形
∵G为EF中点
![]() (等腰三角形的三线合一)
(等腰三角形的三线合一)
又![]() AF平分
AF平分![]() ,
,![]()
![]()
![]() 为等腰直角三角形,
为等腰直角三角形,![]()
![]()
![]()
![]() ,即
,即![]()
在![]() 与
与![]() 中,
中,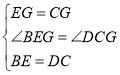
![]()
![]()
![]()
![]()
![]()
![]() 为等腰直角三角形
为等腰直角三角形
![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,交y轴于点E.
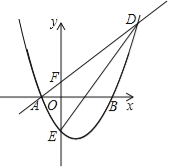
(1)求此抛物线的解析式.
(2)若直线y=x+1与抛物线交于A、D两点,与y轴交于点F,连接DE,求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴的一个交点
轴的一个交点![]() .
.
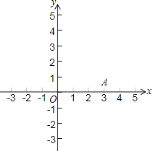
(1)试分别求出这条抛物线与![]() 轴的另一个交点
轴的另一个交点![]() 及与
及与![]() 轴的交点
轴的交点![]() 的坐标.
的坐标.
(2)设抛物线的顶点为![]() ,请在图中画出抛物线的草图,若点
,请在图中画出抛物线的草图,若点![]() 在直线
在直线![]() 上,试判断
上,试判断![]() 点是否在经过
点是否在经过![]() 点的反比例函数的图象上,并说明理由;
点的反比例函数的图象上,并说明理由;
(3)试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数![]() 的图像分别交
的图像分别交![]() 轴、
轴、![]() 轴于
轴于![]() 两点.过点
两点.过点![]() 的直线交
的直线交![]() 轴正半轴于点
轴正半轴于点![]() ,且点
,且点![]() 为线段
为线段![]() 的中点.
的中点.
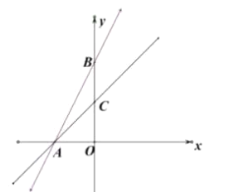
(1)求直线![]() 的表达式;
的表达式;
(2)如果四边形![]() 是平行四边形,求点
是平行四边形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,A(﹣3,0),B(1,b),则正方形ABCD的面积为( )
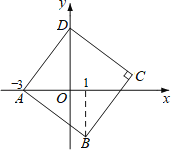
A.34B.25C.20D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题是真命题的是( )
A.两直线平行,同位角相等
B.等边三角形是锐角三角形
C.如果两个实数是正数,那么它们的积是正数
D.全等三角形的对应角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
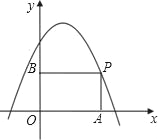
【题目】如图,P是抛物线y=﹣x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com