
【题目】如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732);
≈1.732);
(2)确定C港在A港的什么方向.

【答案】(1)A、C两地之间的距离为14.1km;(2)C港在A港北偏东15°的方向上.
【解析】
(1)根据方位角的定义可得出∠ABC=90°,再根据勾股定理可求得AC的长为14.1.
(2)由(1)可知△ABC为等腰直角三角形,从而得出∠BAC=45°,求出∠CAM=15°,
所而确定C港在A港的什么方向.
(1)由题意可得,∠PBC=30°,∠MAB=60°,∴∠CBQ=60°,∠BAN=30°,∴∠ABQ=30°,∴∠ABC=90°.
∵AB=BC=10,∴AC=![]() =
=![]() ≈14.1.
≈14.1.
答:A、C两地之间的距离为14.1km.
(2)由(1)知,△ABC为等腰直角三角形,∴∠BAC=45°,∴∠CAM=15°,
∴C港在A港北偏东15°的方向上.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润 = 销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
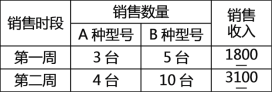
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数 ![]() (件)与价格
(件)与价格 ![]() (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2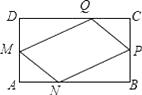
(1)求S关于x的函数关系式,并直接写出自变量x的取值范围.
(2)若a=400,求S的最大值,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC=1,CD=![]() ,DA=1,且∠B=90°.求:
,DA=1,且∠B=90°.求:
(1)∠DAC的度数;
(2)四边形ABCD的面积(结果保留根号);
(3)将△ABC沿AC翻折至△AB′C,如图所示,连接B′D,求△AB′D的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①垂线段最短;②同位角相等;③如果两条直线都与第三条直线平行,那么这两条直线也互相平行;④内错角相等,两直线平行;⑤经过一点有且只有一条直线与已知直线平行;⑥如果![]() =2,那么x=2.其中真命题有( )
=2,那么x=2.其中真命题有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 ![]() 与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线
与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线 ![]() , 则下列结论:① a﹣b+c>0;②b>0;③阴影部分的面积为4;④若c=﹣1,则
, 则下列结论:① a﹣b+c>0;②b>0;③阴影部分的面积为4;④若c=﹣1,则 ![]() . 其中正确的是(写出所有正确结论的序号)
. 其中正确的是(写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com