
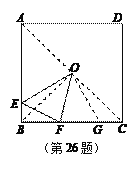
【题目】如图1,点O为正方形ABCD 的中心,E为AB 边上一点,F为BC边上一点,△EBF的周长等于 BC 的长.
(1)求∠EOF 的度数.
(2)连接 OA、OC(如图2).求证:△AOE∽△CFO.
(3)若OE=![]() OF,求
OF,求![]() 的值.
的值.

【答案】(1)45°;(2)证明见解析;(3)![]()
【解析】分析:(1)、在BC上取一点G,使得CG=BE,连接OB、OC、OG,然后证明△OBE和△OCG全等,从而得出∠BOE=∠COG,∠BEO=∠CGO,OE=OG,根据三角形的周长得出EF=GF,从而得出△FOE和△GOF全等,得出∠EOF的度数;(2)、连接OA,根据点O为正方形ABCD的中心得出∠OAE=∠FCO=45°,结合∠BOE=∠COG得出∠AEO=∠COF,从而得出三角形相似;(3)、根据相似得出线段比,根据相似比求出AE和CO的关系,CF和AO的关系,从而得出答案.
详解:解:(1)、如图,在BC上取一点G,使得CG=BE,连接OB、OC、OG.
∵点O为正方形ABCD的中心, ∴ OB=OC,∠BOC=90°,∠OBE=∠OCG=45°.
∴△OBE≌△OCG(SAS). ∴∠BOE=∠COG,∠BEO=∠CGO,OE=OG.
∴∠EOG=90°,∵△BEF的周长等于BC的长,
∴ EF=GF. ∴△EOF≌△GOF(SSS).∴∠EOF=∠GOF=45°.
(2)、连接OA.∵ 点O为正方形ABCD的中心, ∴∠OAE=∠FCO=45°.
∵∠BOE=∠COG, ∠AEO=∠BOE+∠OBE=∠BOE+45°,
∠COF=∠COG+∠GOF=∠COG+45°. ∴ ∠AEO=∠COF,且∠OAE=∠FCO.
∴ △AOE∽△CFO.
(3)、∵△AOE∽△CFO,∴![]() =
=![]() =
=![]() .即AE=
.即AE= ![]() ×CO,CF=AO÷
×CO,CF=AO÷![]() .
.
∵OE=![]() OF,∴
OF,∴![]() =
=![]() .∴AE=
.∴AE=![]() CO,CF=
CO,CF=![]() AO. ∴
AO. ∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某省为推广新能源汽车,计划连续五年给予财政补贴.补贴开始时间为![]() 年度,截止时间为
年度,截止时间为![]() 年度.补贴期间后一年度的补贴额均在前一年度补贴额基础上递增.计划前三年,每年度按固定额度
年度.补贴期间后一年度的补贴额均在前一年度补贴额基础上递增.计划前三年,每年度按固定额度![]() 亿元递增;后两年均在上一年的基础上按相同增长率递增.已知
亿元递增;后两年均在上一年的基础上按相同增长率递增.已知![]() 年度计划补贴额为
年度计划补贴额为![]() 亿元.
亿元.
![]() 若
若![]() 年度计划补贴额比
年度计划补贴额比![]() 年度至少增加
年度至少增加![]() ,求
,求![]() 的取值范围;
的取值范围;
![]() 若预计
若预计![]() 这五年补贴总额比
这五年补贴总额比![]() 年度补贴额的
年度补贴额的![]() 倍还多
倍还多![]() 亿元,求后两年财政补贴的增长率.
亿元,求后两年财政补贴的增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(2x+y)2﹣y(2x+y),其中x=![]() ,y=﹣1;
,y=﹣1;
(2)[(a﹣2b)2+(a﹣2b)(a+2b)﹣2a(2a﹣b)]÷2a,其中a=3,b=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:∠1+∠2_______∠B+∠C(填“>”“<”“=”),当∠A=40°时,∠B+∠C+∠1+∠2=______.
(3)如图③,是由图①的△ABC沿DE折叠得到的,如果∠A=30°,则x+y=360°-(∠B+∠C+∠1+∠2)=360°- = ,猜想∠BDA+∠CEA与∠A的关系为

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】转转盘和摸球是等可能概率下的经典模型.

(1)如图,转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.小莉让转盘自由转动2次,求指针2次都落在黑色区域的概率.
(2)小刚在一个不透明的口袋中,放入除颜色外其余都相同的18个小球,其中4个白球,6个红球,8个黄球.搅匀后,随机摸1个球,若事件A的概率与(1)中概率相同,请写出事件A.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是边BC的中点,CE∥AB,AD平分∠EAB
(1)延长AD、CE相交于点F,求证:AB=CE+AE
(2)当点E和点C重合时,试判断△ABC的形状,请画出图形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com