
【题目】已知![]() 是
是![]() 上一点,
上一点,![]() .
.
(Ⅰ)如图①,过点![]() 作
作![]() 的切线,与
的切线,与![]() 的延长线交于点
的延长线交于点![]() ,求
,求![]() 的大小及
的大小及![]() 的长;
的长;
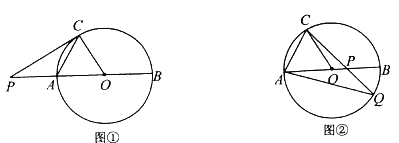
(Ⅱ)如图②,![]() 为
为![]() 上一点,
上一点,![]() 延长线与
延长线与![]() 交于点
交于点![]() ,若
,若![]() ,求
,求![]() 的大小及
的大小及![]() 的长.
的长.
【答案】(Ⅰ)![]() ,PA=4;(Ⅱ)
,PA=4;(Ⅱ)![]() ,
,![]()
【解析】
(Ⅰ)易得△OAC是等边三角形即∠AOC=60°,又由PC是○O的切线故PC⊥OC,即∠OCP=90°可得∠P的度数,由OC=4可得PA的长度
(Ⅱ)由(Ⅰ)知△OAC是等边三角形,易得∠APC=45°;过点C作CD⊥AB于点D,易得AD=![]() AO=
AO=![]() CO,在Rt△DOC中易得CD的长,即可求解
CO,在Rt△DOC中易得CD的长,即可求解
解:(Ⅰ)∵AB是○O的直径,∴OA是○O的半径.
∵∠OAC=60°,OA=OC,∴△OAC是等边三角形.
∴∠AOC=60°.
∵PC是○O的切线,OC为○O的半径,
∴PC⊥OC,即∠OCP=90°∴∠P=30°.
∴PO=2CO=8.
∴PA=PO-AO=PO-CO=4.
(Ⅱ)由(Ⅰ)知△OAC是等边三角形,
∴∠AOC=∠ACO=∠OAC=60°∴∠AQC=30°.
∵AQ=CQ,∴∠ACQ=∠QAC=75°
∴∠ACQ-∠ACO=∠QAC-∠OAC=15°即∠QCO=∠QAO=15°.
∴∠APC=∠AQC+∠QAO=45°.
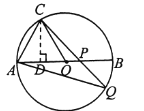
如图②,过点C作CD⊥AB于点D.
∵△OAC是等边三角形,CD⊥AB于点D,
∴∠DCO=30°,AD=![]() AO=
AO=![]() CO=2.
CO=2.
∵∠APC=45°,∴∠DCQ=∠APC=45°
∴PD=CD
在Rt△DOC中,OC=4,∠DCO=30°,∴OD=2,∴CD=2![]()
∴PD=CD=2![]()
∴AP=AD+DP=2+2![]()


科目:初中数学 来源: 题型:
【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
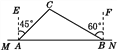
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点A(-1,0),点B(-3,0),且OB=OC,
轴交于点A(-1,0),点B(-3,0),且OB=OC,
(1)求抛物线的解析式;
(2)点P在抛物线上,且∠POB=∠ACB,求点P的坐标;
(3)抛物线上两点M,N,点M的横坐标为m,点N的横坐标为m+4.点D是抛物线上M,N之间的动点,过点D作y轴的平行线交MN于点E.
①求DE的最大值.
②点D关于点E的对称点为F.当m为何值时,四边形MDNF为矩形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.

依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图①所示,将直尺摆放在三角板ABC上,使直尺与三角板的边分别交于点D,E,F,G,量得∠CGD=42°。

(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示.点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“一带一路”战略给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年人均收入人民币2600元,预计2018年人均收入将达到人民币13000元,设2016年到2018年该地区居民人均收入平均增长率为x,可列方程为( ).
A.2600(1+2x)=13000B.2600(1+x)2=13000
C.2600(1+x2)=13000D.2600+2x=13000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生英语听力训练情况(七、八年级学生人数相同),某周从这两个年级学生中分别随机抽查了30名同学,调查了他们周一至周五的听力训练情况,根据调查情况得到如下统计图表:周一至周五英语听力训练人数统计表
年级 | 参加英语听力训练人数 | ||||
周一 | 周二 | 周三 | 周四 | 周五 | |
七年级 | 15 | 20 |
| 30 | 30 |
八年级 | 20 | 24 | 26 | 30 | 30 |
合计 | 35 | 44 | 51 | 60 | 60 |

(1)填空:![]() ________;
________;
(2)根据上述统计图表完成下表中的相关统计量:
年级 | 平均训练时间的中位数 | 参加英语听力训练人数的方差 |
七年级 | 24 | 34 |
八年级 | 14.4 |
(3)请你利用上述统计图表,对七、八年级英语听力训练情况写出两条合理的评价;
(4)请你结合周一至周五英语听力训练人数统计表,估计该校七、八年级共480名学生中周一至周五平均每天有多少人进行英语听力训练.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组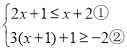 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得____________________;
(Ⅱ)解不等式②,得_______________________;
(III)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l : y kx b k 0 与曲线有 n 个交点,则称直线l 为曲线的“ n 阶共生直线”,交点称为它们的“共生点”.
(1)若直线 y kx b k 0与某曲线的一个“共生点”为 P m, 2m 1,试判断此“共生点”不可能位于第几象限,请说明理由.
(2)若直线 l : y kx 2k k 0 与 x 、 y 轴分别交于 A 、 B 两点,且直线 l 为反比例函数y=![]() 的“ 2阶共生直线”,且“共生点”为C、D
的“ 2阶共生直线”,且“共生点”为C、D![]() ,求k的取值范围,试证明此时不论 k 取何值,总有 AC BD 成立.
,求k的取值范围,试证明此时不论 k 取何值,总有 AC BD 成立.
(3)若直线l : y kx 2k k 0 与 x 轴交于点 A ,且直线l 为抛物线 y x2 2x 1的“2 阶共生直线”,且“共生点”为 P 、Q xP xQ ,若 AQ 3AP ,求 k 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com