
【题目】若直线l : y kx b k 0 与曲线有 n 个交点,则称直线l 为曲线的“ n 阶共生直线”,交点称为它们的“共生点”.
(1)若直线 y kx b k 0与某曲线的一个“共生点”为 P m, 2m 1,试判断此“共生点”不可能位于第几象限,请说明理由.
(2)若直线 l : y kx 2k k 0 与 x 、 y 轴分别交于 A 、 B 两点,且直线 l 为反比例函数y=![]() 的“ 2阶共生直线”,且“共生点”为C、D
的“ 2阶共生直线”,且“共生点”为C、D![]() ,求k的取值范围,试证明此时不论 k 取何值,总有 AC BD 成立.
,求k的取值范围,试证明此时不论 k 取何值,总有 AC BD 成立.
(3)若直线l : y kx 2k k 0 与 x 轴交于点 A ,且直线l 为抛物线 y x2 2x 1的“2 阶共生直线”,且“共生点”为 P 、Q xP xQ ,若 AQ 3AP ,求 k 的值.
【答案】(1)不经过第四象限,(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]()
【解析】
(1)直线y=2x+1不经过第四象限,故得答案;
(2)过点C作CE⊥ OA ,过点D作DF⊥OA,DH⊥OB,列方程组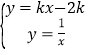 整理得一个一元二次方程,由交点数可知方程有两个不相等的实数根,故△=
整理得一个一元二次方程,由交点数可知方程有两个不相等的实数根,故△= ![]() 可求得K的取值范围,然后求得A(2,0),设
可求得K的取值范围,然后求得A(2,0),设![]() ,解得
,解得![]() ,故AE=OF=DH,证得△ACE≌△DHB,得出AC=BD,所以此时不论 k 取何值,总有 AC BD 成立;
,故AE=OF=DH,证得△ACE≌△DHB,得出AC=BD,所以此时不论 k 取何值,总有 AC BD 成立;
(3)作出图形,则有![]() ,列出方程解得
,列出方程解得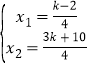 ,又因为
,又因为![]() ,所以
,所以![]() ,求解可得k值.
,求解可得k值.
解:(1)∵P(m,2m+1)在直线y=2x+1上,它不经过第四象限,
∴P不可能位于第四象限.
(2)如图,过点C作CE⊥ OA ,过点D作DF⊥OA,DH⊥OB,
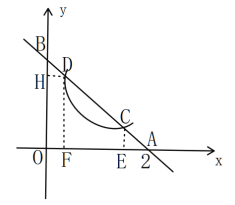
由题意列方程组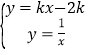 ,整理得
,整理得![]() ,
,
因为有2个交点,故方程有两个不相等的实数根,
∴△= ![]()
解得![]()
令y=0,得x=2,所以A(2,0)
设![]()
∴![]()
∴![]()
∴AE=OF=DH
又∵AC,BD在同一直线上,易得△ACE≌△DHB
∴AC=BD
∴此时不论 k 取何值,总有 AC BD 成立.
(3)如图
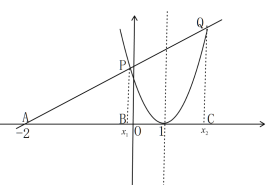
![]()
又![]()
∴![]()
∴![]()
∴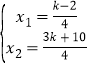
又∵![]()
∴![]()
∴![]()
∴![]() (负值舍去)
(负值舍去)
得![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,过点A作半圆O的切线交BC的延长线于点F,连结BE,AD
(1)求证:∠F=∠EBC;
(2)若AE=2,tan∠EAD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解八年级学生参加社会实践活动情况,某区教育部门随机调查了本区部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
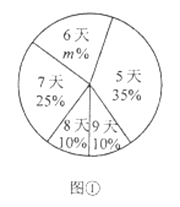

(I)本次接受随机抽样调查的学生人数为_______________,图①中的m的为______________
(Ⅱ)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)若该区八年级学生有300人,估计参加社会实践活动时间大于7天的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
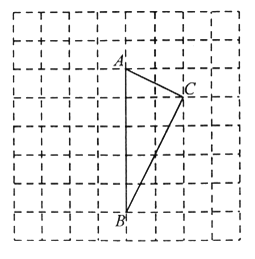
【题目】如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上,
(I)△ABC是_____________三角形(填“锐角”、“直角”或“钝角”):
(Ⅱ)若P,Q分别为边AB,BC上的动点,当PC+PQ取得最小值时,在如图所示的网格中,用无刻度的直尺,画出线段PC,PQ,并简要说明点2的位置是如何找到的(不要求证明).
________________________________________________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有()个
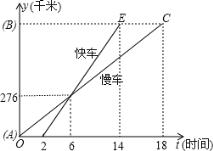
①快车追上慢车需6小时
②慢车比快车早出发2小时
③快车速度为46km/h
④慢车速度为46km/h
⑤AB两地相距828km
⑥快车14小时到达B地
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com