
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��40Ԫ������ۼ�Ϊÿ��50Ԫ��ÿ���¿�����210��������ۼ۳���50Ԫ��������80Ԫ��ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ��������1��������ۼ۳���80Ԫ�������Ǽۣ���ÿ��1Ԫÿ������3������ÿ����Ʒ���ۼ�ΪxԪ��ÿ���µ�������Ϊy����
��1����y��x�ĺ�����ϵʽ��ֱ��д���Ա���x��ȡֵ��Χ��
��2����ÿ�µ���������ΪW����ֱ��д��W��x�ĺ�����ϵʽ��
��3��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ��������������������Ƕ���Ԫ��
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3���ۼ۶�Ϊ90Ԫ���������Ϊ7500Ԫ.
����3���ۼ۶�Ϊ90Ԫ���������Ϊ7500Ԫ.
��������
(1)���ۼ۳���50Ԫ��������80Ԫ��ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ��������1����y=260-x(50��x��80)��������ۼ۳���80Ԫ�������Ǽۣ���ÿ��1Ԫÿ������3����y=420-3x(80��x��140)��
��2��������=���ۼ�-�ɱ������������г�������ϵʽ��
��3���ֱ���������������ں��������ֵ��Ȼ�����Ƚ�.
�⣺![]() ��
��![]() ʱ��
ʱ��![]() ����
����![]() ��
��
��![]() ʱ��
ʱ��![]() ����
����![]() ��
��
��![]() ��
��
![]() ������
������![]() ���ۼ�-�ɱ���
���ۼ�-�ɱ���![]() �����������г�������ϵʽ��
�����������г�������ϵʽ��
![]() ��
��
![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��![]() �����ֵ�����ֵΪ
�����ֵ�����ֵΪ![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ�������ֵ�����ֵΪ
ʱ�������ֵ�����ֵΪ![]() ��
��
���ۼ۶�Ϊ![]() Ԫ���������Ϊ
Ԫ���������Ϊ![]() Ԫ��
Ԫ��
�ʴ�Ϊ����1��![]() ����2��
����2��![]() ��
��![]() ����3���ۼ۶�Ϊ90Ԫ���������Ϊ7500Ԫ.
����3���ۼ۶�Ϊ90Ԫ���������Ϊ7500Ԫ.


 ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
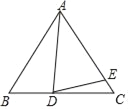
����Ŀ����֪��ABC��AB=AC��DΪֱ��BC��һ�㣬EΪֱ��AC��һ�㣬AD=AE�����BAD=������CDE=�£�
(1)��ͼ������D���߶�BC�ϣ���E���߶�AC�ϣ�
�������ABC=60�㣬��ADE=70������ô��=�� ���㣬��=�� ���㣻
����������֮��Ĺ�ϵʽ��
(2)��ֱ��д����ͬ�����Ϣ��е�������֮��Ĺ�ϵʽ�������� ������д��һ�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������һ���ϵ����߽�������������ε��ܳ���Ϊ9![]() ��15
��15![]() �����֣���������������ε�����Ϊ__________
�����֣���������������ε�����Ϊ__________![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
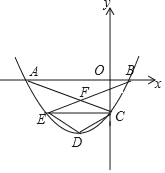
����Ŀ����ͼ��������y=mx2+2mx+n����A����3��0����C��0����![]() �����㣬��x�ύ����һ��B��
�����㣬��x�ύ����һ��B��
��1����A��B��C����������ߵĽ���ʽ��
��2������C��CE��x�ύ�������ڵ�E��д����E�����꣬����AC��BE�Ľ���F������
��3���������ߵĶ���ΪD������DC��DE���ı���CDEF�Ƿ�Ϊ���Σ����ǣ���֤���������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ������
������![]() ��
��
(1)��֤��![]() Ϊ�������ʵ��ʱ��������
Ϊ�������ʵ��ʱ��������![]() ��
��![]() ������������ͬ�Ľ��㣻
������������ͬ�Ľ��㣻
(2)��������![]() ��
��![]() ���������������꣨�ú�
���������������꣨�ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
(3)��������![]() ��
��![]() ��������ƽ��һ����λ���ȵõ�������
��������ƽ��һ����λ���ȵõ�������![]() ��������
��������![]() ȡ�κη���ʵ����
ȡ�κη���ʵ����![]() ������ͬһ�����㣬ֱ��д�������������꣮
������ͬһ�����㣬ֱ��д�������������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ�������й���У�����������ִ������ߡ����в����ݳ����ɼ�����ѡ��5��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ�����������Ӹ�ѡ����5��ѡ�ֵľ����ɼ���ͼ��ʾ��

��1������ͼʾ��д�±���
ƽ�������֣� | ��λ�����֣� | �������֣� | |
���в� | 85 | ||
���в� | 85 | 100 |
��2��������ӳɼ���ƽ��������λ���������ĸ��ӵľ����ɼ��Ϻã�
��3���������Ӿ����ɼ��ķ���ж���һ��������ѡ�ֳɼ���Ϊ�ȶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
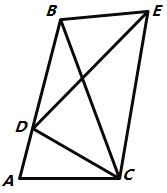
����Ŀ����ͼ����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת�õ�
˳ʱ����ת�õ�![]() ��ʹ��
��ʹ��![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ǡ�����ڱ�
ǡ�����ڱ�![]() �ϣ���
�ϣ���![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ������
������![]() ����������
����������![]() ����
����![]() ����
����![]() ����
����![]() ���ĸ����ۣ������һ����ȷ���У� ����
���ĸ����ۣ������һ����ȷ���У� ����
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����![]() ��
��![]() (
(![]() �dz���,��
�dz���,��![]() )��ͬһƽ��ֱ������ϵ��ͼ������ǣ� ��
)��ͬһƽ��ֱ������ϵ��ͼ������ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90������б��AB��һ��OΪԲ�ģ�OBΪ�뾶����O����AC�ڵ�E����AB�ڵ�D���ҡ�BEC=��BDE��
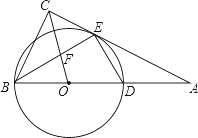
��1����֤��AC�ǡ�O�����ߣ�
��2������OC��BE�ڵ�F����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com