
【题目】已知抛物线![]() ,其中
,其中![]() .
.
(1)求证:![]() 为任意非零实数时,抛物线
为任意非零实数时,抛物线![]() 与
与![]() 轴总有两个不同的交点;
轴总有两个不同的交点;
(2)求抛物线![]() 与
与![]() 轴的两个交点的坐标(用含
轴的两个交点的坐标(用含![]() 的代数式表示);
的代数式表示);
(3)将抛物线![]() 沿
沿![]() 轴正方向平移一个单位长度得到抛物线
轴正方向平移一个单位长度得到抛物线![]() ,则无论
,则无论![]() 取任何非零实数,
取任何非零实数,![]() 都经过同一个定点,直接写出这个定点的坐标.
都经过同一个定点,直接写出这个定点的坐标.
【答案】(1)证明见解析;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)令y=0,利用根的判别式证明即可;
(2) 令y=0,解关于x的一元二次方程即可得到两个交点的坐标;
(3) 根据平移的规律得出C2的解析式y=mx2+x,求出抛物线与y轴的交点即可.
解:(1)证明:令y=0,则![]() =0,
=0,
△=b2-4ac=(2m+1)2-4m(m+1)=4m2+4m+1-4m2-4m=1>0,
∴![]() 为任意非零实数时,抛物线
为任意非零实数时,抛物线![]() 与
与![]() 轴总有两个不同的交点;
轴总有两个不同的交点;
(2) 令y=0,则![]() =0,
=0,
这里a=m,b=2m+1,c=m+1,
∵△=b2-4ac=(2m+1)2-4m(m+1)=4m2+4m+1-4m2-4m=1,
∴![]() ,
,
解得:x1=![]() ,x2=-1,
,x2=-1,
∴抛物线![]() 与
与![]() 轴的两个交点的坐标是
轴的两个交点的坐标是![]() ,
,![]() .
.
![]() ∵将抛物线
∵将抛物线![]() 沿
沿![]() 轴正方向平移一个单位长度得到抛物线
轴正方向平移一个单位长度得到抛物线![]() ,且抛物线
,且抛物线![]() ,
,
∴![]() ,
,
∴无论![]() 取任何非零实数,
取任何非零实数,![]() 都经过同一个定点
都经过同一个定点![]() ,
,
答:无论![]() 取任何非零实数,
取任何非零实数,![]() 都经过同一个定点,这个定点的坐标是
都经过同一个定点,这个定点的坐标是![]() .
.
故答案为:(1)证明见解析;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
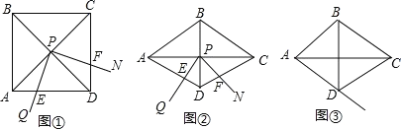
【题目】如图①,∠QPN的顶点P在正方形ABCD两条对角线交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是________;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为________,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,当点E落在线段AD的延长线上时,探究DE,DF,AD之间的数量关系(直接写出结论,不用加以证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
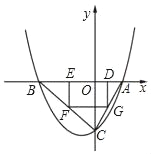
【题目】如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(2,0)、B(﹣4,0)两点,与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC、AC上.
(I)求抛物线的解析式;
(II)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系式,并指出m的取值范围;
(III)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF.若点M在抛物线上,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
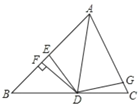
A. 6B. 12C. 4D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)育德中学800名学生参加第二十届运动会开幕式大型表演,道具选用红黄两色锦绣手幅.已知红色手幅每个4元;黄色手幅每个2.5元;购买800个道具共花费2420元,那么两种手幅各多少个?
(2)学校计划制作1000个吉祥物作为运动会纪念.现有甲、乙两个工厂可以生产这种吉祥物.
甲工厂报价:不超过400个时每个吉祥物20元,400个以上超过部分打七折;但因生产条件限制,截止到学校交货日期只能完成800个;乙工厂报价每个吉祥物18元,但需运费400元.问:学校怎样安排生产可以使总花费最少,最少多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com