
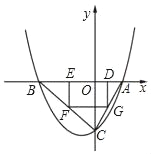
【题目】如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(2,0)、B(﹣4,0)两点,与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC、AC上.
(I)求抛物线的解析式;
(II)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系式,并指出m的取值范围;
(III)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF.若点M在抛物线上,求k的值.
【答案】(I)y=![]() x2+x﹣4;(II)S矩形DEFG=12m﹣6m2(0<m<2);(III)点M在抛物线上,此时k的值是:k=
x2+x﹣4;(II)S矩形DEFG=12m﹣6m2(0<m<2);(III)点M在抛物线上,此时k的值是:k=![]() .
.
【解析】
(I)用待定系数法,将A、B的坐标代入y=ax2+bx﹣4,即可得到抛物线的解析式;
(II)表示出矩形的长和宽是解题的关键,由△ADG∽△AOC,从而![]() =
=![]() ,得到DG=4-2m,由△BEF∽△BOC,从而
,得到DG=4-2m,由△BEF∽△BOC,从而![]() =
=![]() ,得到DE=3m,因而得到S与m的函数关系式;
,得到DE=3m,因而得到S与m的函数关系式;
(III)当矩形的面积s取最大值时,就是函数的值是最大值时,根据二次函数的性质就可以求出相应的m的值,则矩形的四个顶点的坐标就可以求出,利用待定系数法就可以求出直线DF的解析式,便可求出直线DF与抛物线的交点M坐标,过M作x轴的垂线交x轴于H,有△OEF∽△OHM,则根据FM=kDF,即k=![]() =
=![]() ,便可求出k的值.
,便可求出k的值.
(I)∵抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(2,0)、B(﹣4,0)两点,
∴![]() ,
,
解得: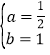 ,
,
故抛物线解析式为:y=![]() x2+x﹣4;
x2+x﹣4;
(II)由题意,![]() =
=![]() ,而AO=2,OC=4,AD=2﹣m,
,而AO=2,OC=4,AD=2﹣m,
故DG=4﹣2m,
又![]() =
=![]() ,EF=DG,得BE=4﹣2m,
,EF=DG,得BE=4﹣2m,
∴DE=3m,
∴S矩形DEFG=DGDE=(4﹣2m)3m=12m﹣6m2(0<m<2).
(III)∵S矩形DEFG=12m﹣6m2(0<m<2),
∴m=1时,矩形的面积最大,且最大面积是6.
当矩形面积最大时,其顶点为D(1,0),G(1,﹣2),F(﹣2,﹣2),E(﹣2,0),
设直线DF的解析式为y=kx+b,
则![]() ,
,
解得;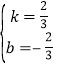 ,
,
∴y=![]() x﹣
x﹣![]() ,
,
又抛物线P的解析式为:y=![]() x2+x﹣4,
x2+x﹣4,
令![]() x﹣
x﹣![]() =
=![]() x2+x﹣4,可求出x=
x2+x﹣4,可求出x=![]()
设射线DF与抛物线P相交于点M,则M的横坐标为![]() ,
,
过M作x轴的垂线交x轴于H,
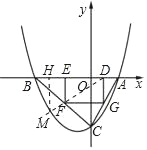
有k=![]() =
=![]() =
=![]() =
=![]() ,
,
点M在抛物线上,此时k的值是:k=![]() .
.
故答案为:(I)y=![]() x2+x﹣4;(II)S矩形DEFG=12m﹣6m2(0<m<2);(III)点M在抛物线上,此时k的值是:k=
x2+x﹣4;(II)S矩形DEFG=12m﹣6m2(0<m<2);(III)点M在抛物线上,此时k的值是:k=![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案科目:初中数学 来源: 题型:
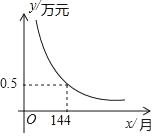
【题目】为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
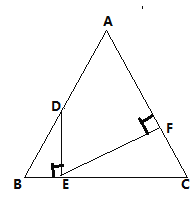
【题目】如图,等边△ABC的边长为12, D为AB边上一动点,过点D作DE⊥BC于点E.过点E作EF⊥AC于点F.
(1)若AD=2,求AF的长;
(2)当AD取何值时,DE=EF?
查看答案和解析>>
科目:初中数学 来源: 题型:
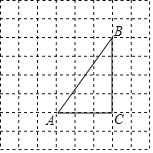
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(1)计算△ABC的周长等于_____.
(2)点P、点Q(不与△ABC的顶点重合)分别为边AB、BC上的动点,4PB=5QC,连接AQ、PC.当AQ⊥PC时,请在如图所示的网格中,用无刻度的直尺,画出线段AQ、PC,并简要说明点P、Q的位置是如何找到的(不要求证明).
___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx的图象与正比例函数y=kx的图象相交于点A(3,2),有下面四个结论:①ab>0;②a﹣b>﹣![]() ;③sinα=
;③sinα=![]() ;④不等式kx≤ax2+bx的解集是0≤x≤3.其中正确的是( )
;④不等式kx≤ax2+bx的解集是0≤x≤3.其中正确的是( )
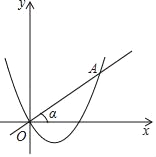
A. ①② B. ②③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,其中
,其中![]() .
.
(1)求证:![]() 为任意非零实数时,抛物线
为任意非零实数时,抛物线![]() 与
与![]() 轴总有两个不同的交点;
轴总有两个不同的交点;
(2)求抛物线![]() 与
与![]() 轴的两个交点的坐标(用含
轴的两个交点的坐标(用含![]() 的代数式表示);
的代数式表示);
(3)将抛物线![]() 沿
沿![]() 轴正方向平移一个单位长度得到抛物线
轴正方向平移一个单位长度得到抛物线![]() ,则无论
,则无论![]() 取任何非零实数,
取任何非零实数,![]() 都经过同一个定点,直接写出这个定点的坐标.
都经过同一个定点,直接写出这个定点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com