
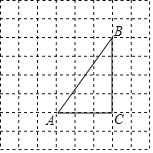
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(1)计算△ABC的周长等于_____.
(2)点P、点Q(不与△ABC的顶点重合)分别为边AB、BC上的动点,4PB=5QC,连接AQ、PC.当AQ⊥PC时,请在如图所示的网格中,用无刻度的直尺,画出线段AQ、PC,并简要说明点P、Q的位置是如何找到的(不要求证明).
___________________________.
【答案】12 连接DE与BC与交于点Q,连接DF与BC交于点M,连接GH与格线交于点N,连接MN与AB交于P.
【解析】
(1)利用勾股定理求出AB,从而得到△ABC的周长;
(2) 取格点D,E,F,G,H,连接DE与BC交于点Q;连接DF与BC交于点M;连接GH与格线交于点N;连接MN与AB交于点P;连接AP,CQ即为所求.
解:(1)∵AC=3,BC=4,∠C=90,
∴根据勾股定理得AB=5,
∴△ABC的周长=5+4+3=12.
(2)取格点D,E,F,G,H,连接DE与BC交于点Q;连接DF与BC交于点M;连接GH与格线交于点N;连接MN与AB交于点P;连接AQ,CP即为所求。

故答案为:(1)12;(2)连接DE与BC与交于点Q,连接DF与BC交于点M,连接GH与格线交于点N,连接MN与AB交于P.


科目:初中数学 来源: 题型:
【题目】在长方形纸片ABCD中,点E是边CD上的一点,将△AED沿AE所在的直线折叠,使点D落在点F处.

(1)如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为 °.
(2)如图2,若点F落在边BC上,且AB=6,AD=10,求CE的长.
(3)如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=6,AD=10,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
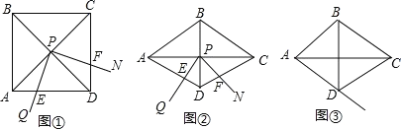
【题目】如图①,∠QPN的顶点P在正方形ABCD两条对角线交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是________;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为________,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,当点E落在线段AD的延长线上时,探究DE,DF,AD之间的数量关系(直接写出结论,不用加以证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在冋一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达日的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
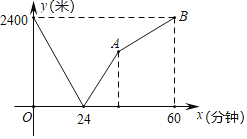
(1)根据图象信息,当t= 分钟时甲乙两人相遇,乙的速度为 米/分钟;
(2)求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.人体构造学的研究成果表明,一般情况下人的指距![]() 和身高
和身高![]() 成如下所示的关系.
成如下所示的关系.

(1)直接写出身高![]() 与指距
与指距![]() 的函数关系式: .
的函数关系式: .
(2)姚明的身高是226厘米,可预测他的指距约为多少?(精确到0.1厘米)
查看答案和解析>>
科目:初中数学 来源: 题型:
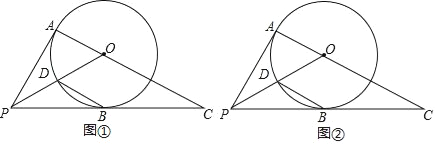
【题目】已知PA、PB是⊙O的切线,A、B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
(1)如图①,若∠AOP=65°,求∠C的大小;
(2)如图②,连接BD,若BD∥AC,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
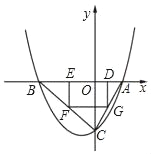
【题目】如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(2,0)、B(﹣4,0)两点,与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC、AC上.
(I)求抛物线的解析式;
(II)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系式,并指出m的取值范围;
(III)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF.若点M在抛物线上,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com