
【题目】在长方形纸片ABCD中,点E是边CD上的一点,将△AED沿AE所在的直线折叠,使点D落在点F处.

(1)如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为 °.
(2)如图2,若点F落在边BC上,且AB=6,AD=10,求CE的长.
(3)如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=6,AD=10,求CG的长.
【答案】(1)18;(2)CE的长为![]() ;(3)CG的长为
;(3)CG的长为![]() .
.
【解析】
(1)由矩形的性质可知∠BAD=90°,易知∠DAC的度数,由折叠的性质可知∠DAE=![]() ∠DAC,计算可得∠DAE的度数.
∠DAC,计算可得∠DAE的度数.
(2)由矩形四个角都是直角及对边相等的性质及折叠后图形对应边相等的性质,结合勾股定理可得BF长,由CF=BC﹣BF可求出CF长,设CE=x,则EF=ED=6﹣x,在Rt△CEF中,根据勾股定理求出x值即可;
(3)连接EG,由中点及折叠的性质利用HL定理可证Rt△CEG≌△FEG,结合全等三角形对应边相等的性质可设CG=FG=y,可用含y的代数式表示出AG、BG,在Rt△ABG中,根据勾股定理求解即可.
解:(1)∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠BAC=54°,
∴∠DAC=90°﹣54°=36°,
由折叠的性质得:∠DAE=∠FAE,
∴∠DAE=![]() ∠DAC=18°;
∠DAC=18°;
故答案为:18;
(2)∵四边形ABCD是矩形,
∴∠B=∠C=90°,BC=AD=10,CD=AB=6,
由折叠的性质得:AF=AD=10,EF=ED,
∴BF=![]() =
=![]() =8,
=8,
∴CF=BC﹣BF=10﹣8=2,
设CE=x,则EF=ED=6﹣x,
在Rt△CEF中,由勾股定理得:22+x2=(6﹣x)2,
解得:x=![]() ,
,
即CE的长为![]() ;
;
(3)连接EG,如图3所示:
∵点E是CD的中点,
∴DE=CE,
由折叠的性质得:AF=AD=10,∠AFE=∠D=90°,FE=DE,
∴∠EFG=90°=∠C,
在Rt△CEG和△FEG中,
![]() ,
,
∴Rt△CEG≌△FEG(HL),
∴CG=FG,
设CG=FG=y,
则AG=AF+FG=10+y,BG=BC﹣CG=10﹣y,
在Rt△ABG中,由勾股定理得:62+(10﹣y)2=(10+y)2,
解得:y=![]() ,
,
即CG的长为![]() .
.



科目:初中数学 来源: 题型:
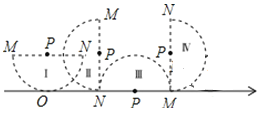
【题目】如图,有一直径MN=4的半圆形纸片,其圆心为点P,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅳ,其中位置Ⅰ中的MN平行于数轴,且半⊙P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上.
解答下列问题:
(1)位置Ⅰ中的MN与数轴之间的距离为____________;
(2)位置Ⅱ中的半⊙P与数轴的位置关系是________;
(3)求位置Ⅲ中的圆心P在数轴上表示的数;
(4)纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时,求该纸片所扫过图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
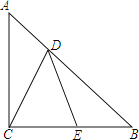
【题目】△ABC中,AC=BC,∠ACB=90°,点D在AB上,点E在BC上,且AD=BE,BD=AC,连DE、CD.
(1)找出图中全等图形,并证明;
(2)求∠ACD的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
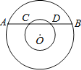
【题目】如图,两同心圆中,大圆的弦![]() 交小圆于
交小圆于![]() 、
、![]() 两点,点
两点,点![]() 到
到![]() 的距离等于
的距离等于![]() 的一半,且
的一半,且![]() .则大小圆的半径之比为( )
.则大小圆的半径之比为( )
A. ![]() :1 B. 2:
:1 B. 2:![]() C. 10:
C. 10:![]() D. 3:1
D. 3:1
查看答案和解析>>
科目:初中数学 来源: 题型:
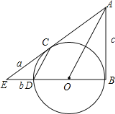
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 与
与![]() 相切于点
相切于点![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .
.
![]() 试探究
试探究![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 已知
已知![]() ,
,![]() ,
,![]() ,请你思考后,选用以上适当的数据,设计出计算
,请你思考后,选用以上适当的数据,设计出计算![]() 的半径
的半径![]() 的一种方案:①你选用的已知数是________;②写出求解过程.(结果用字母表示)
的一种方案:①你选用的已知数是________;②写出求解过程.(结果用字母表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
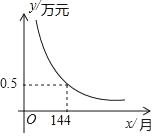
【题目】为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(1﹣2m)x+m+1及坐标平面内一点P(2,0);
(1)若一次函数图象经过点P(2,0),求m的值;
(2)若一次函数的图象经过第一、二、三象限;
①求m的取值范围;
②若点M(a﹣1,y1),N(a,y2),在该一次函数的图象上,则y1 y2(填“>”、”=”、”<”).
查看答案和解析>>
科目:初中数学 来源: 题型:
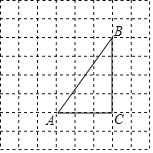
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(1)计算△ABC的周长等于_____.
(2)点P、点Q(不与△ABC的顶点重合)分别为边AB、BC上的动点,4PB=5QC,连接AQ、PC.当AQ⊥PC时,请在如图所示的网格中,用无刻度的直尺,画出线段AQ、PC,并简要说明点P、Q的位置是如何找到的(不要求证明).
___________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com