
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 与
与![]() 相切于点
相切于点![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .
.
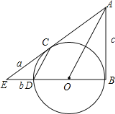
![]() 试探究
试探究![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 已知
已知![]() ,
,![]() ,
,![]() ,请你思考后,选用以上适当的数据,设计出计算
,请你思考后,选用以上适当的数据,设计出计算![]() 的半径
的半径![]() 的一种方案:①你选用的已知数是________;②写出求解过程.(结果用字母表示)
的一种方案:①你选用的已知数是________;②写出求解过程.(结果用字母表示)
科目:初中数学 来源: 题型:
【题目】阅读:
对于两个不等的非零实数![]() .若分式
.若分式![]() 的值为零,则
的值为零,则![]() 或
或![]() 又因为
又因为![]() .所以关于
.所以关于![]() 的方程
的方程![]() 有两个根分别为
有两个根分别为![]() .
.
应用上面的结论解答下列问题:
(1)方程![]() 的两个解中较小的一个为 .
的两个解中较小的一个为 .
(2)关于解![]() 的方程
的方程![]() ,首先我们两边同加
,首先我们两边同加![]() 成
成![]() ,则
,则![]() 或
或![]() ,两个解分别为
,两个解分别为![]() , 则
, 则![]() ,
,![]() .
.
(3)关于![]() 的方程
的方程![]() 的两个解分别为
的两个解分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P是等边三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB等于( )
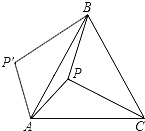
A.150° B.105° C.120° D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
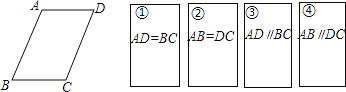
【题目】如图,4张背面完全相同的纸牌(用①、②、③、④表示),在纸牌的正面分别写有四个不同的条件,小明将这4张纸牌背面朝上洗匀后,先随机摸出一张(不放回),再随机摸出一张.
(1)用树状图(或列表法)表示两次摸牌出现的所有可能结果;
(2)以两次摸出牌上的结果为条件,求能判断四边形ABCD是平行四边形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形纸片ABCD中,点E是边CD上的一点,将△AED沿AE所在的直线折叠,使点D落在点F处.

(1)如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为 °.
(2)如图2,若点F落在边BC上,且AB=6,AD=10,求CE的长.
(3)如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=6,AD=10,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=6,点E是边CD上的动点(点E不与端点C,D重合),AE的垂直平分线FG分别交AD,AE,BC于点F,H,G.当![]() =
=![]() 时,DE的长为( )
时,DE的长为( )

A. 2 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
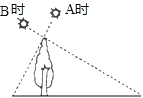
【题目】如图,在 A 时测得某树(垂直于地面)的影长为 4 米,B 时又测得该树的影长为 16 米,若两次日 照的光线互相垂直,则树的高度为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲,乙两名自行车骑手均从P地出发,骑车前往距P地60千米的Q地,当乙骑手出发了1.5小时,此时甲,乙两名骑手相距6千米,因甲骑手接到紧急任务,故甲到达Q地后立即又原路返回P地甲,乙两名骑手距P地的路程y(千米)与时间x(时)的函数图象如图所示.(其中折线O﹣A﹣B﹣C﹣D(实线)表示甲,折线O﹣E﹣F﹣G(虚线)表示乙)
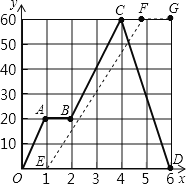
(1)甲骑手在路上停留 小时,甲从Q地返回P地时的骑车速度为 千米/时;
(2)求乙从P地到Q地骑车过程中(即线段EF)距P地的路程y(千米)与时间x(时)的函数关系式及自变量x的取值范围;
(3)在乙骑手出发后,且在甲,乙两人相遇前,求时间x(时)的值为多少时,甲,乙两骑手相距8千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
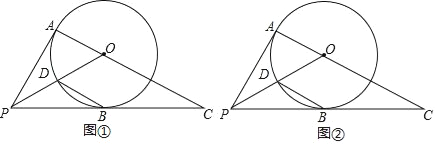
【题目】已知PA、PB是⊙O的切线,A、B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
(1)如图①,若∠AOP=65°,求∠C的大小;
(2)如图②,连接BD,若BD∥AC,求∠C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com