
【题目】如图所示,点P是等边三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB等于( )
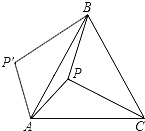
A.150° B.105° C.120° D.90°
【答案】A
【解析】
试题先根据等边三角形的性质得AB=AC,∠BAC=60°,再根据旋转的性质得∠P′AP=60°,P′B=CP=10,AP′=AP=6,则可判断△APP′为等边三角形,得到∠APP′=60°,PP′=AP=6,接着利用勾股定理的逆定理证明△PBP′为直角三角形,∠P′PB=90°,然后利用∠APB=∠APP′+∠P′PB进行计算即可.
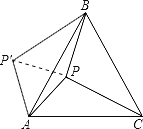
解:连结PP′,如图,
∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠P′AP=60°,P′B=CP=10,AP′=AP=6,
∴△APP′为等边三角形,
∴∠APP′=60°,PP′=AP=6,
在△BPP′中,∵BP=8,PP′=6,P′B=10,
∴PP′2+PB2=P′B2,
∴△PBP′为直角三角形,∠P′PB=90°,
∴∠APB=∠APP′+∠P′PB=60°+90°=150°.
故选A.


科目:初中数学 来源: 题型:
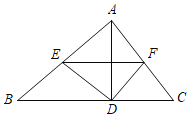
【题目】如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)AB=12,AC=9,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
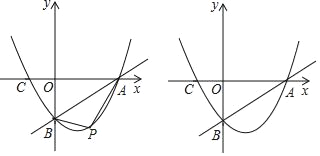
【题目】已知:直线y=![]() x﹣3与x轴、y轴分别交于点A、B,抛物线y=
x﹣3与x轴、y轴分别交于点A、B,抛物线y=![]() x2+bx+c经过点A、B,且交x轴于点C.
x2+bx+c经过点A、B,且交x轴于点C.
(1)求抛物线的解析式;
(2)点P为抛物线上一点,且点P在AB的下方,设点P的横坐标为m.
①试求当m为何值时,△PAB的面积最大;
②当△PAB的面积最大时,过点P作x轴的垂线PD,垂足为点D,问在直线PD上否存在点Q,使△QBC为直角三角形?若存在,直接写出符合条件的Q的坐标若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
售价(元/台) | 月销售量(台) |
400 | 200 |
250 | |
x |
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
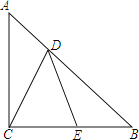
【题目】△ABC中,AC=BC,∠ACB=90°,点D在AB上,点E在BC上,且AD=BE,BD=AC,连DE、CD.
(1)找出图中全等图形,并证明;
(2)求∠ACD的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
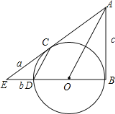
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 与
与![]() 相切于点
相切于点![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .
.
![]() 试探究
试探究![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 已知
已知![]() ,
,![]() ,
,![]() ,请你思考后,选用以上适当的数据,设计出计算
,请你思考后,选用以上适当的数据,设计出计算![]() 的半径
的半径![]() 的一种方案:①你选用的已知数是________;②写出求解过程.(结果用字母表示)
的一种方案:①你选用的已知数是________;②写出求解过程.(结果用字母表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
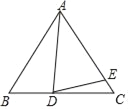
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α= °,β= °;
②求α,β之间的关系式.
(2)请直接写出不同于以上②中的α,β之间的关系式可以是 .(写出一个即可.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com