
【题目】已知![]() 中,边
中,边![]() 的长与
的长与![]() 边上的高的和为
边上的高的和为![]() ,当
,当![]() 面积最大时,则其周长的最小值为________(用含
面积最大时,则其周长的最小值为________(用含![]() 的代数式表示).
的代数式表示).
【答案】![]()
【解析】
设BC上的高为x,则BC=a﹣x,△ABC的面积为S,S=![]() x(a﹣x),根据二次函数的顶点坐标,可得出x的值,过点A作直线l∥BC,再作出点B关于直线l的对称点E,连接CE,交l于点F,可得△CBE是直角三角形,根据勾股定理求出CE的长,从而得出周长的最小值.
x(a﹣x),根据二次函数的顶点坐标,可得出x的值,过点A作直线l∥BC,再作出点B关于直线l的对称点E,连接CE,交l于点F,可得△CBE是直角三角形,根据勾股定理求出CE的长,从而得出周长的最小值.
设BC上的高为x.
∵边BC的长与BC边上的高的和为a,∴BC=a﹣x,设△ABC的面积为S,∴S=![]() x(a﹣x)=﹣
x(a﹣x)=﹣![]() x2+
x2+![]() ax.
ax.
∵当△ABC面积最大时,∴x=![]() a,∴BC=
a,∴BC=![]() a,过点A作直线l∥BC,再作出点B关于直线l的对称点E,连接CE,交l于点F,当点A与点F重合时,△ABC周长的最小值,∴BG=GE=AD=
a,过点A作直线l∥BC,再作出点B关于直线l的对称点E,连接CE,交l于点F,当点A与点F重合时,△ABC周长的最小值,∴BG=GE=AD=![]() a,∴BE=a.
a,∴BE=a.
∵直线l∥BC,∴∠EBC=∠EGA=90°,∴CE=![]() =
=![]() a,∴△ABC的最小周长=
a,∴△ABC的最小周长=![]() a.
a.
故答案为:![]() a.
a.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( ).
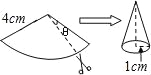
A.0.8πcm2 B.3.2πcm2 C.4πcm2 D.4.8πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:
对于两个不等的非零实数![]() .若分式
.若分式![]() 的值为零,则
的值为零,则![]() 或
或![]() 又因为
又因为![]() .所以关于
.所以关于![]() 的方程
的方程![]() 有两个根分别为
有两个根分别为![]() .
.
应用上面的结论解答下列问题:
(1)方程![]() 的两个解中较小的一个为 .
的两个解中较小的一个为 .
(2)关于解![]() 的方程
的方程![]() ,首先我们两边同加
,首先我们两边同加![]() 成
成![]() ,则
,则![]() 或
或![]() ,两个解分别为
,两个解分别为![]() , 则
, 则![]() ,
,![]() .
.
(3)关于![]() 的方程
的方程![]() 的两个解分别为
的两个解分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 港在
港在![]() 地的正南
地的正南![]() 千米处,一艘轮船由
千米处,一艘轮船由![]() 港开出向西航行,某人第一次在
港开出向西航行,某人第一次在![]() 处望见该船在南偏西
处望见该船在南偏西![]() ,半小时后,又望见该船在南偏西
,半小时后,又望见该船在南偏西![]() ,则该船速度为________千米/小时.
,则该船速度为________千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】背景知识:如图,在![]() 中,
中,![]() ,若
,若![]() ,则:
,则:![]() .
.
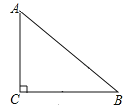
(1)解决问题:
如图(1),![]() ,
,![]() ,
,![]() 是过点
是过点![]() 的直线,过点
的直线,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,现尝试探究线段
,现尝试探究线段![]() 、
、![]() 、
、![]() 之间的数量关系:过点
之间的数量关系:过点![]() 作
作![]() ,与
,与![]() 交于点
交于点![]() ,易发现图中出现了一对全等三角形,即
,易发现图中出现了一对全等三角形,即![]() ,由此可得线段
,由此可得线段![]() 、
、![]() 、
、![]() 之间的数量关系是: ;
之间的数量关系是: ;

(2)类比探究:
将图(1)中的![]() 绕点
绕点![]() 旋转到图(2)的位置,其它条件不变,试探究线段
旋转到图(2)的位置,其它条件不变,试探究线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(3)拓展应用:
将图(1)中的![]() 绕点
绕点![]() 旋转到图 (3)的位置,其它条件不变,若
旋转到图 (3)的位置,其它条件不变,若![]() ,
,![]() ,则
,则![]() 的长为 (直接写结果).
的长为 (直接写结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点P是等边三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则∠APB等于( )
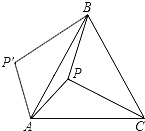
A.150° B.105° C.120° D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
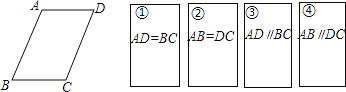
【题目】如图,4张背面完全相同的纸牌(用①、②、③、④表示),在纸牌的正面分别写有四个不同的条件,小明将这4张纸牌背面朝上洗匀后,先随机摸出一张(不放回),再随机摸出一张.
(1)用树状图(或列表法)表示两次摸牌出现的所有可能结果;
(2)以两次摸出牌上的结果为条件,求能判断四边形ABCD是平行四边形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲,乙两名自行车骑手均从P地出发,骑车前往距P地60千米的Q地,当乙骑手出发了1.5小时,此时甲,乙两名骑手相距6千米,因甲骑手接到紧急任务,故甲到达Q地后立即又原路返回P地甲,乙两名骑手距P地的路程y(千米)与时间x(时)的函数图象如图所示.(其中折线O﹣A﹣B﹣C﹣D(实线)表示甲,折线O﹣E﹣F﹣G(虚线)表示乙)
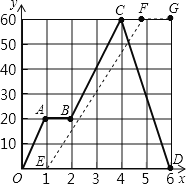
(1)甲骑手在路上停留 小时,甲从Q地返回P地时的骑车速度为 千米/时;
(2)求乙从P地到Q地骑车过程中(即线段EF)距P地的路程y(千米)与时间x(时)的函数关系式及自变量x的取值范围;
(3)在乙骑手出发后,且在甲,乙两人相遇前,求时间x(时)的值为多少时,甲,乙两骑手相距8千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com