
【题目】![]() 港在
港在![]() 地的正南
地的正南![]() 千米处,一艘轮船由
千米处,一艘轮船由![]() 港开出向西航行,某人第一次在
港开出向西航行,某人第一次在![]() 处望见该船在南偏西
处望见该船在南偏西![]() ,半小时后,又望见该船在南偏西
,半小时后,又望见该船在南偏西![]() ,则该船速度为________千米/小时.
,则该船速度为________千米/小时.
科目:初中数学 来源: 题型:
【题目】已知k为任意实数,随着k的变化,抛物线y=x2﹣2(k﹣1)x+k2﹣5的顶点随之运动,则顶点运动时经过的路径与两条坐标轴围成图形的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.
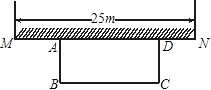
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,AD=6,E.F分别是线段AD,BC上的点,连接EF,使四边形ABFE为正方形,若点G是AD上的动点,连接FG,将矩形沿FG折叠使得点C落在正方形ABFE的对角线所在的直线上,对应点为P,则线段AP的长为______.
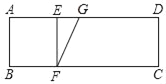
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线y=![]() x﹣3与x轴、y轴分别交于点A、B,抛物线y=
x﹣3与x轴、y轴分别交于点A、B,抛物线y=![]() x2+bx+c经过点A、B,且交x轴于点C.
x2+bx+c经过点A、B,且交x轴于点C.
(1)求抛物线的解析式;
(2)点P为抛物线上一点,且点P在AB的下方,设点P的横坐标为m.
①试求当m为何值时,△PAB的面积最大;
②当△PAB的面积最大时,过点P作x轴的垂线PD,垂足为点D,问在直线PD上否存在点Q,使△QBC为直角三角形?若存在,直接写出符合条件的Q的坐标若不存在,请说明理由.
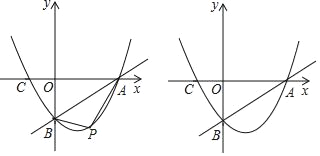
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
售价(元/台) | 月销售量(台) |
400 | 200 |
250 | |
x |
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
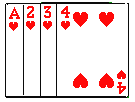
(1)从中随机抽出一张牌,牌面数字是偶数的概率是 ;
(2)从中随机抽出二张牌,两张牌牌面数字的和是5的概率是 ;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com