练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在矩形ABCD中，AB=2，AD=6，E．F分别是线段AD，BC上的点，连接EF，使四边形ABFE为正方形，若点G是AD上的动点，连接FG，将矩形沿FG折叠使得点C落在正方形ABFE的对角线所在的直线上，对应点为P，则线段AP的长为______．

    【答案】4或4﹣2

    【解析】

    当点P在AF上时，由翻折的性质可求得PF=FC=4，然后再求得正方形的对角线AF的长，从而可得到PA的长；当点P在BE上时，由正方形的性质可知BP为AF的垂直平分线，则AP=PF，由翻折的性质可求得PF=FC=4，故此可得到AP的值．

    解：如图1所示：

    由翻折的性质可知PF=CF=4，

    ∵ABFE为正方形，边长为2，

    ∴AF=2．

    ∴PA=4﹣2．

    如图2所示：

    由翻折的性质可知PF=FC=4．

    ∵ABFE为正方形，

    ∴BE为AF的垂直平分线．

    ∴AP=PF=4．

    故答案为：4或4﹣2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四边形中，，为的中点，连接并延长交的延长线于点，连接平分．下列结论：①；②垂直平分；③；④；其中正确的是_____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，∠ACB＝90°，AC＝BC＝4，D是AB的中点，点E是射线CB上的动点，连接DE，DF⊥DE交射线AC于点F．

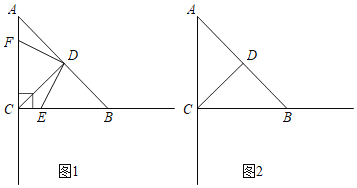
    （1）若点E在线段CB上．

    ①求证：AF＝CE．

    ②连接EF，试用等式表示AF、EB、EF这三条线段的数量关系，并说明理由．

    （2）当EB＝3时，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

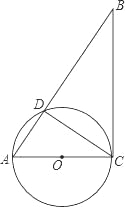
    【题目】如图，在Rt△ABC中，∠ACB=90°，以AC为直径作⊙O交AB于点D点，连接CD．

    （1）求证：∠A=∠BCD；

    （2）若M为线段BC上一点，试问当点M在什么位置时，直线DM与⊙O相切？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读：

    对于两个不等的非零实数．若分式的值为零，则或又因为．所以关于的方程有两个根分别为．

    应用上面的结论解答下列问题：

    （1）方程的两个解中较小的一个为　　　　．

    （2）关于解的方程，首先我们两边同加成，则 或 ，两个解分别为， 则 ， ．

    （3）关于的方程的两个解分别为，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两个筑路队共同承担一段一级路的施工任务，甲队单独施工完成此项任务比乙队单独施工完成此项任务多用15天．且甲队单独施工60天和乙队单独施工40天的工作量相同．

    （1）甲、乙两队单独完成此项任务各需多少天？

    （2）若甲、乙两队共同工作了4天后，乙队因设备检修停止施工，由甲队单独继续施工，为了不影响工程进度，甲队的工作效率提高到原来的2倍，要使甲队总的工作量不少于乙队的工作量的2倍，那么甲队至少再单独施工多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】港在地的正南千米处，一艘轮船由港开出向西航行，某人第一次在处望见该船在南偏西，半小时后，又望见该船在南偏西，则该船速度为________千米/小时．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】背景知识：如图，在中，，若，则：．

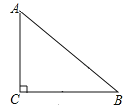
    （1）解决问题：

    如图（1），，，是过点的直线，过点作于点，连接，现尝试探究线段、、 之间的数量关系：过点作，与交于点，易发现图中出现了一对全等三角形，即，由此可得线段、、之间的数量关系是： ；

    （2）类比探究：

    将图（1）中的绕点旋转到图（2）的位置，其它条件不变，试探究线段、、之间的数量关系，并证明；

    （3）拓展应用：

    将图（1）中的绕点旋转到图 （3）的位置，其它条件不变，若，，则的长为 （直接写结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，AD=6，点E是边CD上的动点（点E不与端点C，D重合），AE的垂直平分线FG分别交AD，AE,BC于点F，H，G．当=时，DE的长为（ ）

    A. 2 B. C. D. 4

    查看答案和解析>>

    同步练习册答案