
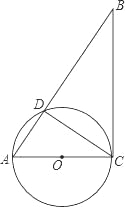
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.
(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.
【答案】(1)证明见试题解析;(2)M为BC的中点.
【解析】试题分析:(1)根据圆周角定理可得∠ADC=90°,再根据直角三角形的性质可得∠A+∠DCA=90°,再由∠DCB+∠ACD=90°,可得∠DCB=∠A;
(2)当MC=MD时,直线DM与⊙O相切,连接DO,根据等等边对等角可得∠1=∠2,∠4=∠3,再根据∠ACB=90°可得∠1+∠3=90°,进而证得直线DM与⊙O相切.
试题解析:(1)∵AC为直径,
∴∠ADC=90°,
∴∠A+∠DCA=90°,
∵∠ACB=90°,
∴∠DCB+∠ACD=90°,
∴∠DCB=∠A;
(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切;
解:连接DO,
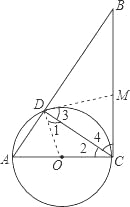
∵DO=CO,
∴∠1=∠2,
∵DM=CM,
∴∠4=∠3,
∵∠2+∠4=90°,
∴∠1+∠3=90°,
∴直线DM与⊙O相切,
故当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】小强在学校组织的社会调查活动中负责了解他所居住的小区 450户居民的家庭收入情况.他从中随机调查了 40 户居民家庭人均收入情况(收入取整数,单位:元), 并绘制了如下的频数分布表和频数分布直方图.


根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭属于中等收入(人均不低于 1000 元但不足 1600 元)的大约 有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
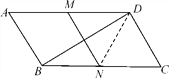
【题目】如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=![]() MN.
MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
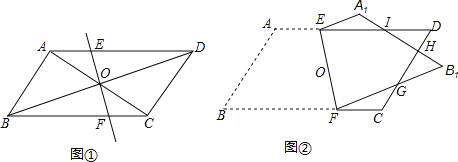
【题目】(1)如图①,ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.
(2)如图②,将ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
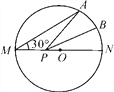
【题目】如图,MN是半径为2的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为( )
A. 4![]() B. 2 C. 4 D. 2
B. 2 C. 4 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
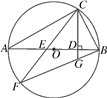
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
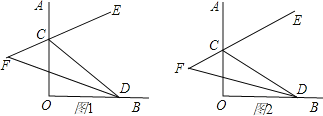
【题目】如图,∠AOB=90°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.
(1)当∠OCD=50°(图1),试求∠F.
(2)当C、D在射线OA、OB上任意移动时(不与点O重合)(图2),∠F的大小是否变化?若变化,请说明理由;若不变化,求出∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一
A:计时制:0.05元/分,B:包月制:50元/月,此外,每一种上网时间都要收通信费0.02元/分
(1)某用户某月上网时间为x小时,请写出两种收费方式下该用户应该支付的费用(用y表示)
(2)若甲用户估计一个月上网时间为20小时,乙用户估计一个月上网时间为15小时,各选哪一种收费方式最合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有5个白球和若干个红球![]() 每个球除颜色外都相同
每个球除颜色外都相同![]() 的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验
的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验![]() 其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
![]() 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少?
![]() 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com