
【题目】将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
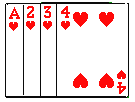
(1)从中随机抽出一张牌,牌面数字是偶数的概率是 ;
(2)从中随机抽出二张牌,两张牌牌面数字的和是5的概率是 ;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
试题(1)共有4种情况,其中数字是偶数的由2种,所以概率为![]() ;(2)共有6种情况,符合要求的有2种,故概率为
;(2)共有6种情况,符合要求的有2种,故概率为![]() =
=![]() ;(3)先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率即可.
;(3)先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率即可.
试题解析:(1)A,2,3,4共有4张牌,随意抽取一张为偶数的概率为![]() =
=![]() ;
;
(2)1+4=5;2+3=5,但组合一共有3+2+1=6,故概率为![]() =
=![]() ;
;
(3)根据题意,画树形图如图所示。
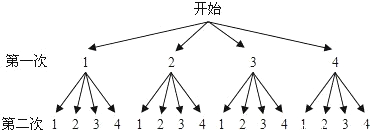
由树形图可知,共有16种等可能的结果:11,12,13,14,21,22,23,24,31,32,33,34,41,42,43,44;其中恰好是4的位数的共有4种:12,24,32,44,所以P(4的倍数)=![]() .
.


科目:初中数学 来源: 题型:
【题目】![]() 港在
港在![]() 地的正南
地的正南![]() 千米处,一艘轮船由
千米处,一艘轮船由![]() 港开出向西航行,某人第一次在
港开出向西航行,某人第一次在![]() 处望见该船在南偏西
处望见该船在南偏西![]() ,半小时后,又望见该船在南偏西
,半小时后,又望见该船在南偏西![]() ,则该船速度为________千米/小时.
,则该船速度为________千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
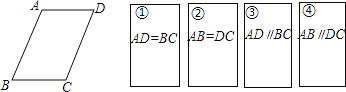
【题目】如图,4张背面完全相同的纸牌(用①、②、③、④表示),在纸牌的正面分别写有四个不同的条件,小明将这4张纸牌背面朝上洗匀后,先随机摸出一张(不放回),再随机摸出一张.
(1)用树状图(或列表法)表示两次摸牌出现的所有可能结果;
(2)以两次摸出牌上的结果为条件,求能判断四边形ABCD是平行四边形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=6,点E是边CD上的动点(点E不与端点C,D重合),AE的垂直平分线FG分别交AD,AE,BC于点F,H,G.当![]() =
=![]() 时,DE的长为( )
时,DE的长为( )

A. 2 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
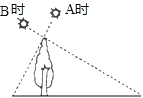
【题目】如图,在 A 时测得某树(垂直于地面)的影长为 4 米,B 时又测得该树的影长为 16 米,若两次日 照的光线互相垂直,则树的高度为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x22(k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲,乙两名自行车骑手均从P地出发,骑车前往距P地60千米的Q地,当乙骑手出发了1.5小时,此时甲,乙两名骑手相距6千米,因甲骑手接到紧急任务,故甲到达Q地后立即又原路返回P地甲,乙两名骑手距P地的路程y(千米)与时间x(时)的函数图象如图所示.(其中折线O﹣A﹣B﹣C﹣D(实线)表示甲,折线O﹣E﹣F﹣G(虚线)表示乙)
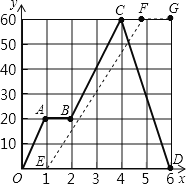
(1)甲骑手在路上停留 小时,甲从Q地返回P地时的骑车速度为 千米/时;
(2)求乙从P地到Q地骑车过程中(即线段EF)距P地的路程y(千米)与时间x(时)的函数关系式及自变量x的取值范围;
(3)在乙骑手出发后,且在甲,乙两人相遇前,求时间x(时)的值为多少时,甲,乙两骑手相距8千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a,b,c表示交叉的三条公路,现要建一货物中转站,要求它到这三条公路的距离相等,则可供选择的站址最多有![]()
![]()

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点F是![]() ABCD的边AD上的三等分点,BF交AC于点E,如果△AEF的面积为2,那么四边形CDFE的面积等于( )
ABCD的边AD上的三等分点,BF交AC于点E,如果△AEF的面积为2,那么四边形CDFE的面积等于( )
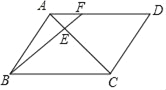
A. 18 B. 22 C. 24 D. 46
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com