【题目】如图，点F是
ABCD的边AD上的三等分点，BF交AC于点E，如果△AEF的面积为2，那么四边形CDFE的面积等于( )
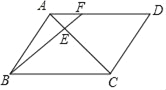
A. 18 B. 22 C. 24 D. 46
【答案】B
【解析】
连接FC，先证明△AEF∽△BEC，得出AE∶EC=1∶3，所以S△EFC=3S△AEF，在根据点F是□ABCD的边AD上的三等分点得出S△FCD=2S△AFC，四边形CDFE的面积=S△FCD+ S△EFC，再代入△AEF的面积为2即可求出四边形CDFE的面积.
∵AD∥BC，
∴∠EAF=∠ACB,∠AFE=∠FBC；
∵∠AEF=∠BEC，
∴△AEF∽△BEC，
∴
=
=
，
∵△AEF与△EFC高相等，
∴S△EFC=3S△AEF，
∵点F是□ABCD的边AD上的三等分点，
∴S△FCD=2S△AFC，
∵△AEF的面积为2，
∴四边形CDFE的面积=S△FCD+ S△EFC=16+6=22.
故答案选B.
科目：初中数学 来源： 题型：
【题目】将如图所示的牌面数字分别是1，2，3，4的四张扑克牌背面朝上，洗匀后放在桌面上．
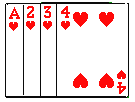
（1）从中随机抽出一张牌，牌面数字是偶数的概率是 ；
（2）从中随机抽出二张牌，两张牌牌面数字的和是5的概率是 ；
（3）先从中随机抽出一张牌，将牌面数字作为十位上的数字，然后将该牌放回并重新洗匀，再随机抽取一张，将牌面数字作为个位上的数字，请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式了的平方，如3+2
＝（1+）2．善于思考的小明进行了以下探索：
若设a+b＝（m+n）2＝m2+2n2+2mn（其中a、b、m、n均为整数），
则有a＝m2+2n2，b＝2mn．
这样小明就找到了一种把类似a+b的式子化为平方式的方法．
请你仿照小明的方法探索并解决下列问题：
（1）若a+b
＝（m+n）2，当a、b、m、n均为整数时，用含m、n的式子分别表示a、b，得：a＝ ，b＝ ；
（2）若a+6
＝（m+n）2，且a、m、n均为正整数，求a的值；
（3）化简：
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
三个顶点的坐标分别为
，
，
．
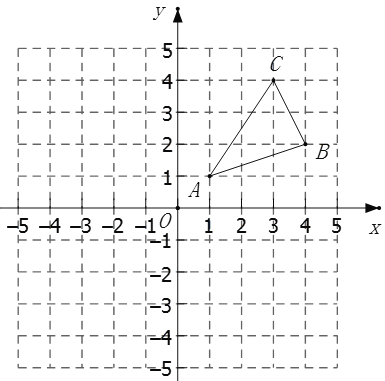
（1）请画出关于
轴成轴对称的图形
，并写出
、
、
的坐标；
（2）求的面积；
（3〉在
轴上找一点
，使
的值最小，请画出点的位置．
查看答案和解析>>
科目：初中数学 来源： 题型：
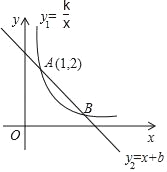
【题目】反比例函数y1=
（x＞0）的图象与一次函数y2=﹣x+b的图象交于A，B两点，其中A（1，2）
（1）求这两个函数解析式；
（2）在y轴上求作一点P，使PA+PB的值最小，并直接写出此时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
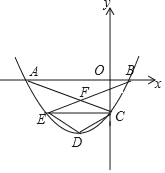
【题目】如图，抛物线y=mx2+2mx+n经过A（﹣3，0），C（0，﹣
）两点，与x轴交于另一点B．
（1）求经过A，B，C三点的抛物线的解析式；
（2）过点C作CE∥x轴交抛物线于点E，写出点E的坐标，并求AC、BE的交点F的坐标
（3）若抛物线的顶点为D，连结DC、DE，四边形CDEF是否为菱形？若是，请证明；若不是，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市某中学举行“中国梦校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如图所示．
（1）根据图示填写下表；
平均数（分） | 中位数（分） | 众数（分） | |
初中部 | 85 | ||
高中部 | 85 | 100 |
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某班将举行“数学知识竞赛”活动，班长安排小明购买奖品，下面两图是小明买回奖品时与班长的对话情境：
请根据上面的信息，解决问题：
(1)试计算两种笔记本各买了多少本？
(2)请你解释：小明为什么不可能找回68元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
