
����Ŀ����֪�ף����������г����־���P�س������ﳵǰ����P��60ǧ��Q�أ��������ֳ�����1.5Сʱ����ʱ�ף��������������6ǧ�ף�������ֽӵ��������ʼ���Q�غ�������ԭ·����P�ؼף����������־�P�ص�·��y��ǧ�ף���ʱ��x��ʱ���ĺ���ͼ����ͼ��ʾ������������O��A��B��C��D��ʵ�ߣ���ʾ�ף�����O��E��F��G�����ߣ���ʾ�ң�
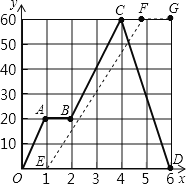
��1����������·��ͣ���� ��Сʱ���״�Q�ط���P��ʱ���ﳵ�ٶ�Ϊ�� ��ǧ��/ʱ��
��2�����Ҵ�P�ص�Q���ﳵ�����У����߶�EF����P�ص�·��y��ǧ�ף���ʱ��x��ʱ���ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��3���������ֳ��������ڼף�����������ǰ����ʱ��x��ʱ����ֵΪ����ʱ���ף������������8ǧ�ף�
���𰸡���1��1Сʱ��30ǧ��/ʱ����2��y=24x��24��1��x��3.5������3��x=![]()
��������
��1������������ͼ���ɣ�
��2������ҵ��ٶȣ������ô���ϵ������ɣ�
��3�����ݣ�2���Ľ����з��̽�ɣ�
��1����ͼ���֪����������·��ͣ��1Сʱ���״�Q�ط���P��ʱ���ﳵ�ٶ�Ϊ��60����6��4��=30��ǧ��/ʱ����
�ʴ�Ϊ��1��30��
��2���״�P�ص�Q�ص��ٶ�Ϊ20��ǧ��/ʱ���������ҵ��ٶ�Ϊ����6+1.5��20����1.5=24��ǧ��/ʱ����
60��24=2.5��Сʱ����
���Ҵ�P�ص�Q���ﳵ�����У����߶�EF����P�ص�·��y��ǧ�ף���ʱ��x��ʱ���ĺ�����ϵʽΪy=24x+b����
24+b=0�����b=��24��
���Ҵ�P�ص�Q���ﳵ�����У����߶�EF����P�ص�·��y��ǧ�ף���ʱ��x��ʱ���ĺ�����ϵʽΪy=24x��24��1��x��3.5����
��3����������ã�
30��x��4��+��24x��24��=60��8��
���x=![]() ��
��
������������ǰ����ʱ��x=![]() ʱ���ף������������8ǧ�ף�
ʱ���ף������������8ǧ�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �У���
����![]() �ij���
�ij���![]() ���ϵĸߵĺ�Ϊ
���ϵĸߵĺ�Ϊ![]() ����
����![]() ������ʱ�������ܳ�����СֵΪ________���ú�
������ʱ�������ܳ�����СֵΪ________���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
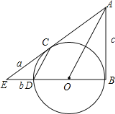
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() �����ڵ�
�����ڵ�![]() ������
������![]() ��
��![]() ��ƽ���߽�
��ƽ���߽�![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ���ӳ����ཻ�ڵ�
���ӳ����ཻ�ڵ�![]() ��
��
![]() ��̽��
��̽��![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
![]() ��֪
��֪![]() ��
��![]() ��
��![]() ������˼����ѡ�������ʵ������ݣ���Ƴ�����
������˼����ѡ�������ʵ������ݣ���Ƴ�����![]() �İ뾶
�İ뾶![]() ��һ�ַ���������ѡ�õ���֪����________����д�������̣����������ĸ��ʾ��
��һ�ַ���������ѡ�õ���֪����________����д�������̣����������ĸ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ���������ֱַ���1��2��3��4�������˿��Ʊ��泯�ϣ�ϴ�Ⱥ���������ϣ�
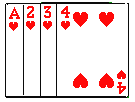
��1������������һ���ƣ�����������ż���ĸ����� ��
��2�����������������ƣ��������������ֵĺ���5�ĸ����� ��
��3���ȴ���������һ���ƣ�������������Ϊʮλ�ϵ����֣�Ȼ���ƷŻز�����ϴ�ȣ��������ȡһ�ţ�������������Ϊ��λ�ϵ����֣����û���״ͼ���б��ķ�������ɵ���λ��ǡ����4�ı����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y����1��2m��x+m+1������ƽ����һ��P��2��0����
��1����һ�κ���ͼ����P��2��0������m��ֵ��
��2����һ�κ�����ͼ����һ�����������ޣ�
����m��ȡֵ��Χ��
������M��a��1��y1����N��a��y2�����ڸ�һ�κ�����ͼ���ϣ���y1�� ��y2������������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
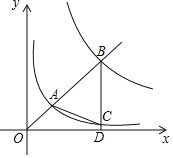
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ֱ֪��y��kx��k��0���ֱ���������y��![]() ��y��
��y��![]() �ڵ�һ����ͼ���ڵ�A��B������B��BD��x���ڵ�D����y��
�ڵ�һ����ͼ���ڵ�A��B������B��BD��x���ڵ�D����y��![]() ��ͼ���ڵ�C������AC������ABC�ǵ��������Σ���k��ֵ��_____��
��ͼ���ڵ�C������AC������ABC�ǵ��������Σ���k��ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC��AB=AC��DΪֱ��BC��һ�㣬EΪֱ��AC��һ�㣬AD=AE�����BAD=������CDE=�£�
(1)��ͼ������D���߶�BC�ϣ���E���߶�AC�ϣ�
�������ABC=60�㣬��ADE=70������ô��=�� ���㣬��=�� ���㣻
����������֮��Ĺ�ϵʽ��
(2)��ֱ��д����ͬ�����Ϣ��е�������֮��Ĺ�ϵʽ�������� ������д��һ�����ɣ���
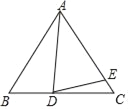
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�С����ѧϰ���θ�ʽ����һЩ�����ŵ�ʽ�ӿ���д����һ��ʽ�˵�ƽ������3+2![]() ����1+
����1+![]() ��2������˼����С������������̽����
��2������˼����С������������̽����
����a+b![]() ����m+n
����m+n![]() ��2��m2+2n2+2mn
��2��m2+2n2+2mn![]() ������a��b��m��n����������
������a��b��m��n����������
����a��m2+2n2��b��2mn��
����С�����ҵ���һ�ְ�����a+b![]() ��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
�������С���ķ���̽��������������⣺
��1����a+b![]() ����m+n
����m+n![]() ��2����a��b��m��n��Ϊ����ʱ���ú�m��n��ʽ�ӷֱ��ʾa��b���ã�a���� ����b���� ����
��2����a��b��m��n��Ϊ����ʱ���ú�m��n��ʽ�ӷֱ��ʾa��b���ã�a���� ����b���� ����
��2����a+6![]() ����m+n
����m+n![]() ��2����a��m��n��Ϊ����������a��ֵ��
��2����a��m��n��Ϊ����������a��ֵ��
��3������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=mx2+2mx+n����A����3��0����C��0����![]() �����㣬��x�ύ����һ��B��
�����㣬��x�ύ����һ��B��
��1����A��B��C����������ߵĽ���ʽ��
��2������C��CE��x�ύ�������ڵ�E��д����E�����꣬����AC��BE�Ľ���F������
��3���������ߵĶ���ΪD������DC��DE���ı���CDEF�Ƿ�Ϊ���Σ����ǣ���֤���������ǣ���˵�����ɣ�
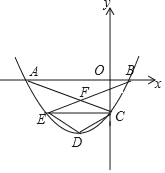
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com