
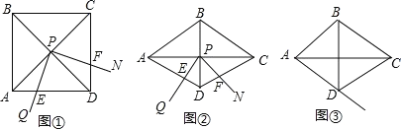
【题目】如图①,∠QPN的顶点P在正方形ABCD两条对角线交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是________;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为________,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,当点E落在线段AD的延长线上时,探究DE,DF,AD之间的数量关系(直接写出结论,不用加以证明).
【答案】(1)DE+DF=AD;(2)DE+DF=![]() AD,证明见解析;(3)DF﹣DE=
AD,证明见解析;(3)DF﹣DE=![]() AD,证明见解析.
AD,证明见解析.
【解析】
(1)根据题意通过“角边角”证明△APE≌△DPF,得到AE=DF,则可得DE+DF=AD;
(2)如图②,取AD的中点M,连接PM,根据题意可证得△MDP是等边三角形,进而可通过“角边角”证明△MPE≌△DPF,得到ME=DF,则可得DE+DF=![]() AD;
AD;
(3)如图③,当点E落在AD的延长线上时,取AD的中点M,连接PM,同理(2)可证得△MPE≌△DPF,得到ME=DF,则可得DF﹣DE=![]() AD.
AD.
(1)正方形ABCD的对角线AC,BD交于点P,
∴PA=PD,∠PAE=∠PDF=45°,
∵∠APE+∠EPD=∠DPF+∠EPD=90°,
∴∠APE=∠DPF,
在△APE和△DPF中,
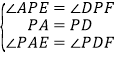 ,
,
∴△APE≌△DPF(ASA),
∴AE=DF,
∴DE+DF=AD;
(2)如图②,取AD的中点M,连接PM,
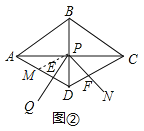
∵四边形ABCD为菱形,∠ADC=120°,
∴AD=CD,∠DAP=30°,AC⊥BD,
∴∠ADP=∠CDP=60°,
∵AM=MD,
∴PM=MD,
∴△MDP是等边三角形,
∴PM=PD,∠MPD=∠PME=∠PDF=60°,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△PME和△DPF中,
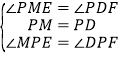 ,
,
∴△MPE≌△DPF(ASA),
∴ME=DF,
∴DE+DF=![]() AD;
AD;
(3)如图③,当点E落在AD的延长线上时,取AD的中点M,连接PM,
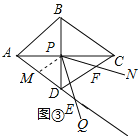
同(2)可证得,△MDP是等边三角形,
∴∠PME=∠MPD=60°,PM=PD,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中,
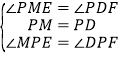 ,
,
∴△MPE≌△DPF(ASA).
∴ME=DF,
∴DF-DE=ME-DE=DM=![]() AD.
AD.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
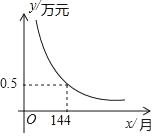
【题目】为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(1﹣2m)x+m+1及坐标平面内一点P(2,0);
(1)若一次函数图象经过点P(2,0),求m的值;
(2)若一次函数的图象经过第一、二、三象限;
①求m的取值范围;
②若点M(a﹣1,y1),N(a,y2),在该一次函数的图象上,则y1 y2(填“>”、”=”、”<”).
查看答案和解析>>
科目:初中数学 来源: 题型:
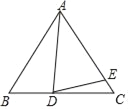
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α= °,β= °;
②求α,β之间的关系式.
(2)请直接写出不同于以上②中的α,β之间的关系式可以是 .(写出一个即可.)
查看答案和解析>>
科目:初中数学 来源: 题型:
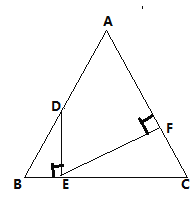
【题目】如图,等边△ABC的边长为12, D为AB边上一动点,过点D作DE⊥BC于点E.过点E作EF⊥AC于点F.
(1)若AD=2,求AF的长;
(2)当AD取何值时,DE=EF?
查看答案和解析>>
科目:初中数学 来源: 题型:
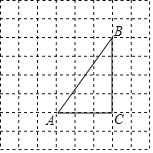
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(1)计算△ABC的周长等于_____.
(2)点P、点Q(不与△ABC的顶点重合)分别为边AB、BC上的动点,4PB=5QC,连接AQ、PC.当AQ⊥PC时,请在如图所示的网格中,用无刻度的直尺,画出线段AQ、PC,并简要说明点P、Q的位置是如何找到的(不要求证明).
___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,其中
,其中![]() .
.
(1)求证:![]() 为任意非零实数时,抛物线
为任意非零实数时,抛物线![]() 与
与![]() 轴总有两个不同的交点;
轴总有两个不同的交点;
(2)求抛物线![]() 与
与![]() 轴的两个交点的坐标(用含
轴的两个交点的坐标(用含![]() 的代数式表示);
的代数式表示);
(3)将抛物线![]() 沿
沿![]() 轴正方向平移一个单位长度得到抛物线
轴正方向平移一个单位长度得到抛物线![]() ,则无论
,则无论![]() 取任何非零实数,
取任何非零实数,![]() 都经过同一个定点,直接写出这个定点的坐标.
都经过同一个定点,直接写出这个定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com