
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
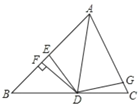
A. 6B. 12C. 4D. 8
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx的图象与正比例函数y=kx的图象相交于点A(3,2),有下面四个结论:①ab>0;②a﹣b>﹣![]() ;③sinα=
;③sinα=![]() ;④不等式kx≤ax2+bx的解集是0≤x≤3.其中正确的是( )
;④不等式kx≤ax2+bx的解集是0≤x≤3.其中正确的是( )
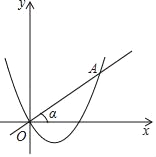
A. ①② B. ②③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度与我们的生活息息相关,如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉).设摄氏温度为x(℃)华氏温度为y(℉),则y是x的一次函数,通过观察我们发现,温度计上的摄氏温度为0℃时,华氏温度为32℉;摄氏温度为﹣20℃时,华氏温度为﹣4℉

请根据以上信息,解答下列问题
(1)仔细观察图中数据,试求出y与x的函数关系式;
(2)当摄氏温度为﹣5℃时,华氏温度为多少?
(3)当华氏温度为59℉时,摄氏温度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,其中
,其中![]() .
.
(1)求证:![]() 为任意非零实数时,抛物线
为任意非零实数时,抛物线![]() 与
与![]() 轴总有两个不同的交点;
轴总有两个不同的交点;
(2)求抛物线![]() 与
与![]() 轴的两个交点的坐标(用含
轴的两个交点的坐标(用含![]() 的代数式表示);
的代数式表示);
(3)将抛物线![]() 沿
沿![]() 轴正方向平移一个单位长度得到抛物线
轴正方向平移一个单位长度得到抛物线![]() ,则无论
,则无论![]() 取任何非零实数,
取任何非零实数,![]() 都经过同一个定点,直接写出这个定点的坐标.
都经过同一个定点,直接写出这个定点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
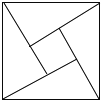
【题目】如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为![]() ,较短直角边长为
,较短直角边长为![]() ,若
,若![]() ,大正方形的面积为13,则小正方形的面积为________.
,大正方形的面积为13,则小正方形的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车与慢车分别从甲、乙两地同时相向出发,匀速而行,快车到达乙地后停留![]() ,然后原路按原速返回,此时,快车比慢车晚
,然后原路按原速返回,此时,快车比慢车晚![]() 到达甲地,快、慢两车距各自出发地的路程
到达甲地,快、慢两车距各自出发地的路程![]() 与所用的时
与所用的时![]() 的关系如图所示.
的关系如图所示.
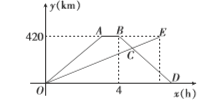
(1)甲、乙两地之间的路程为____________![]() .
.
(2)求![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围.
的取值范围.
(3)当快、慢两车相距![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
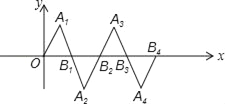
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com