
【题目】为了了解八年级学生参加社会实践活动情况,某区教育部门随机调查了本区部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
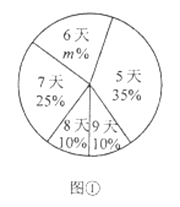

(I)本次接受随机抽样调查的学生人数为_______________,图①中的m的为______________
(Ⅱ)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)若该区八年级学生有300人,估计参加社会实践活动时间大于7天的学生人数。
【答案】(I)80,20;(Ⅱ)众数为5,中位数为6,平均数是6.4;(Ⅲ)该区3000名八年级学生中参加社会实践活动的时间大于7天的人数约为600人
【解析】
(1)由参加7天社会实践的人数除以其占的比例可得到总人数;用16除以总人数即可求m;
(2) 平均数=![]() ,出现次数最多的数据为众数,将数据从小到大排列最中间的就是中位数;
,出现次数最多的数据为众数,将数据从小到大排列最中间的就是中位数;
(3)总人数乘以7天占的比例即可求解.
(I)20÷25%=80,
![]() ,则m=20;
,则m=20;
(Ⅱ)∵在这组样本数据中,5出现了28次,出现的次数最多,
∴这组样本数据的众数为5
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是6,有![]() ,
,
∴这组样本数据的中位数为6
观察条形统计图,![]()
∴这组数据的平均数是6.4
(Ⅲ)∵在80名学生中,参加社会实践活动的时间大于7天的人数比例为![]() ,
,
∴由样本数据,估计该区3000名八年级学生中参加社会实践活动的时间大于7天的人数比例约为![]() ,于是,有
,于是,有![]()
∴该区3000名八年级学生中参加社会实践活动的时间大于7天的人数约为600人


科目:初中数学 来源: 题型:
【题目】某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.

依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组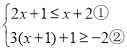 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得____________________;
(Ⅱ)解不等式②,得_______________________;
(III)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
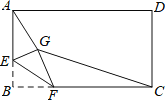
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l : y kx b k 0 与曲线有 n 个交点,则称直线l 为曲线的“ n 阶共生直线”,交点称为它们的“共生点”.
(1)若直线 y kx b k 0与某曲线的一个“共生点”为 P m, 2m 1,试判断此“共生点”不可能位于第几象限,请说明理由.
(2)若直线 l : y kx 2k k 0 与 x 、 y 轴分别交于 A 、 B 两点,且直线 l 为反比例函数y=![]() 的“ 2阶共生直线”,且“共生点”为C、D
的“ 2阶共生直线”,且“共生点”为C、D![]() ,求k的取值范围,试证明此时不论 k 取何值,总有 AC BD 成立.
,求k的取值范围,试证明此时不论 k 取何值,总有 AC BD 成立.
(3)若直线l : y kx 2k k 0 与 x 轴交于点 A ,且直线l 为抛物线 y x2 2x 1的“2 阶共生直线”,且“共生点”为 P 、Q xP xQ ,若 AQ 3AP ,求 k 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为改善办学条件,计划购进![]() 两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
A | 240 | 0 | 210 | 20 |
B | 300 | 0 | 250 | 30 |
(Ⅰ)如果在线下购买![]() 两种书架20个,共花费5520元,求
两种书架20个,共花费5520元,求![]() 两种书架各购买了多少个;
两种书架各购买了多少个;
(Ⅱ)如果在线上购买![]() 两种书架20个,共花费
两种书架20个,共花费![]() 元,设其中
元,设其中![]() 种书架购买
种书架购买![]() 个,求W关于
个,求W关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)在(Ⅱ)的条件下,若购买![]() 种书架的数量不少于
种书架的数量不少于![]() 种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.
种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
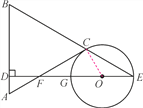
【题目】如图,△ABC中,AB=AC,点E是线段BC延长线上一点,ED⊥AB,垂足为D,ED交线段AC于点F,点O在线段EF上,⊙O经过C、E两点,交ED于点G.
(1)求证:AC是⊙O的切线;
(2)若∠E=30°,AD=1,BD=5,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com