
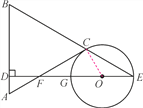
【题目】如图,△ABC中,AB=AC,点E是线段BC延长线上一点,ED⊥AB,垂足为D,ED交线段AC于点F,点O在线段EF上,⊙O经过C、E两点,交ED于点G.
(1)求证:AC是⊙O的切线;
(2)若∠E=30°,AD=1,BD=5,求⊙O的半径.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案科目:初中数学 来源: 题型:
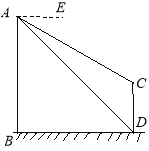
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图13-1至图13-5,⊙O均作无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c.
阅读理解:
(1)如图13-1,⊙O从⊙O1的位置出发,沿AB滚动到⊙O2的位置,当AB=c时,⊙O恰好自转1周.

(2)如图13-2,∠ABC相邻的补角是n°,⊙O在∠ABC外部沿A-B-C滚动,在点B处,必须由⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋转的角∠O1BO2 = n°,⊙O在点B处自转![]() 周.
周.

实践应用:
(1)在阅读理解的(1)中,若AB=2c,则⊙O自转 周;若AB=l,则⊙O自转 周.在阅读理解的(2)中,若∠ABC= 120°,则⊙O在点B处自转 周;若∠ABC= 60°,则⊙O在点B处自转 周.
(2)如图13-3,∠ABC=90°,AB=BC=![]() c.⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转 周.
c.⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转 周.

拓展联想:
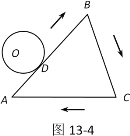
(1)如图13-4,△ABC的周长为l,⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由.
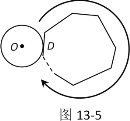
(2)如图13-5,多边形的周长为l,⊙O从与某边相切于点D的位置出发,在多边形外部,按顺时针方向沿多边形滚动,又回到与该边相切于点D的位置,直接写出⊙O自转的周数.
查看答案和解析>>
科目:初中数学 来源: 题型:
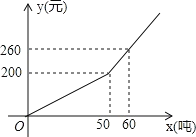
【题目】已知某市2018年企业每月用水量![]() (吨)与该月应缴的水费
(吨)与该月应缴的水费![]() (元)之间的函数关系如图.
(元)之间的函数关系如图.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若某企业2018年10月份的水费为![]() 元,求该企业2018年10月份的用水量;
元,求该企业2018年10月份的用水量;
(3)为贯彻省委发展战略,鼓励企业节约用水,该市自2019年1月开始对月用水量超过![]() 吨的企业加收污水处理费,规定:若企业月用水量
吨的企业加收污水处理费,规定:若企业月用水量![]() 超过
超过![]() 吨,则除按2018年收费标准收取水费外,超过
吨,则除按2018年收费标准收取水费外,超过![]() 吨部分每吨另加收
吨部分每吨另加收![]() 元,若某企业2019年3月份的水费和污水处理费共
元,若某企业2019年3月份的水费和污水处理费共![]() 元,求这个企业该月的用水量.
元,求这个企业该月的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场今年2月份营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.若设商场3月份到5月份营业额的月平均增长率为x,则下面列出的方程中正确的是( )
A.633.6(1+x)2=400(1+10%)B.633.6(1+2x)2=400×(1010%)
C.400×(1+10%)(1+2x)2=633.6D.400×(1+10%)(1+x)2=633.6
查看答案和解析>>
科目:初中数学 来源: 题型:
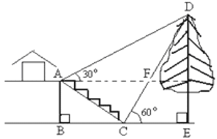
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需资金6000元;若购进3部甲型号手机和2部乙型号手机,共需资金4600元.
(1)求甲、乙型号手机每部进价多少元?
(2)为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.8万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
(3)若甲型号手机的售价为1500元,乙型号手机的售价为1400元,为了促销,公司决定每售出一部乙型号手机,返还顾客现金a元;而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=![]() x2+bx+c经过点A(-1,0),B(5,0).
x2+bx+c经过点A(-1,0),B(5,0).

(1)求抛物线的解析式并写出顶点M的坐标;
(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com