
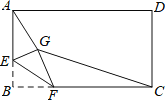
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
【答案】![]() .
.
【解析】
先确定出EG⊥AC时,四边形AGCD的面积最小,再用锐角三角函数求出点G到AC的距离,最后用面积之和即可得出结论.
解:∵四边形ABCD是矩形,
∴CD=AB=3,AD=BC=4,∠ABC=∠D=90°,根据勾股定理得,AC=5,
∵AB=3,AE=2,
∴点F在BC上的任何位置时,点G始终在AC的下方,
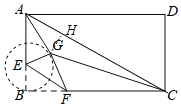
设点G到AC的距离为h,
∵S四边形AGCD=S△ACD+S△ACG=![]() AD×CD+
AD×CD+![]() AC×h=
AC×h=![]() ×4×3+
×4×3+![]() ×5×h=
×5×h=![]() h+6,
h+6,
∴要四边形AGCD的面积最小,即h最小,
∵点G是以点E为圆心,BE=1为半径的圆上在矩形ABCD内部的一部分点,
∴EG⊥AC时,h最小,即点E,点G,点H共线.
由折叠知∠EGF=∠ABC=90°,
延长EG交AC于H,则EH⊥AC,
在Rt△ABC中,sin∠BAC=![]() ,
,
在Rt△AEH中,AE=2,sin∠BAC=![]() =
=![]() ,
,
∴EH=![]() ,AE=
,AE=![]() ,
,
∴h=EH﹣EG=![]() ﹣1=
﹣1=![]() ,
,
∴S四边形AGCD最小=![]() h+6=
h+6=![]() +6=
+6=![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
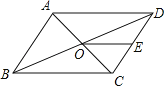
A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(0,4)和(1,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A在直线y=![]() x﹣1上,则点B与点O′之间的距离为( )
x﹣1上,则点B与点O′之间的距离为( )
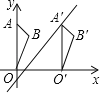
A.3B.4C.3![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,过点A作半圆O的切线交BC的延长线于点F,连结BE,AD
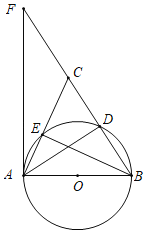
(1)求证:∠F=∠EBC;
(2)若AE=2,tan∠EAD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地下停车场的设计大大缓解了住宅小区停车难的问题,如图是龙泉某小区的地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小刚认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小刚和小亮谁说得对?请你判断并计算出正确的限制高度.(结果精确到0.1m,参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.325)
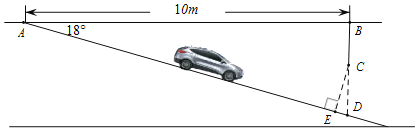
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解八年级学生参加社会实践活动情况,某区教育部门随机调查了本区部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
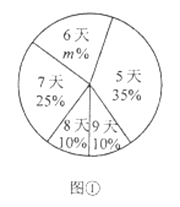

(I)本次接受随机抽样调查的学生人数为_______________,图①中的m的为______________
(Ⅱ)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)若该区八年级学生有300人,估计参加社会实践活动时间大于7天的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
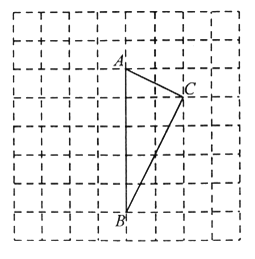
【题目】如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上,
(I)△ABC是_____________三角形(填“锐角”、“直角”或“钝角”):
(Ⅱ)若P,Q分别为边AB,BC上的动点,当PC+PQ取得最小值时,在如图所示的网格中,用无刻度的直尺,画出线段PC,PQ,并简要说明点2的位置是如何找到的(不要求证明).
________________________________________________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点C(O,4),与
轴交于点C(O,4),与![]() 轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴
轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴![]() 与抛物线交于点D,与直线BC交于点E.
与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线Z与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com