
【题目】如图,抛物线![]() 与
与![]() 轴交于点C(O,4),与
轴交于点C(O,4),与![]() 轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴
轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴![]() 与抛物线交于点D,与直线BC交于点E.
与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线Z与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标。

【答案】(1)抛物线的解析式是![]() ;
;
(2)不存在满足条件的点F;
(3)满足条件的点P有三个,分别是P1 (3,1),P2(2+![]() ,2 -
,2 -![]() ),P3(2—
),P3(2—![]() ,2十
,2十![]() )
)
【解析】
试题(1)先把C(0,4)代入y=ax2+bx+c,得出c=4①,再由抛物线的对称轴x=-![]() =1,得到b=-2a②,抛物线过点A(-2,0),得到0=4a-2b+c③,然后由①②③可解得,a=-
=1,得到b=-2a②,抛物线过点A(-2,0),得到0=4a-2b+c③,然后由①②③可解得,a=-![]() ,b=1,c=4,即可求出抛物线的解析式为y=-
,b=1,c=4,即可求出抛物线的解析式为y=-![]() x2+x+4;(2)假设存在满足条件的点F,连结BF、CF、OF,过点F作FH⊥x轴于点H,FG⊥y轴于点G.设点F的坐标为(t,-
x2+x+4;(2)假设存在满足条件的点F,连结BF、CF、OF,过点F作FH⊥x轴于点H,FG⊥y轴于点G.设点F的坐标为(t,-![]() t2+t+4),则FH=-
t2+t+4),则FH=-![]() t2+t+4,FG=t,先根据三角形的面积公式求出S△OBF=
t2+t+4,FG=t,先根据三角形的面积公式求出S△OBF=![]() OBFH=-t2+2t+8,S△OFC=
OBFH=-t2+2t+8,S△OFC=![]() OCFG=2t,再由S四边形ABFC=S△AOC+S△OBF+S△OFC,得到S四边形ABFC=-t2+4t+12.令-t2+4t+12=17,即t2-4t+5=0,由△=(-4)2-4×5=-4<0,得出方程t2-4t+5=0无解,即不存在满足条件的点F;
OCFG=2t,再由S四边形ABFC=S△AOC+S△OBF+S△OFC,得到S四边形ABFC=-t2+4t+12.令-t2+4t+12=17,即t2-4t+5=0,由△=(-4)2-4×5=-4<0,得出方程t2-4t+5=0无解,即不存在满足条件的点F;
(3)先运用待定系数法求出直线BC的解析式为y=-x+4,再求出抛物线y=-![]() x2+x+4的顶点D(1,
x2+x+4的顶点D(1,![]() ),由点E在直线BC上,得到点E(1,3),于是DE=
),由点E在直线BC上,得到点E(1,3),于是DE=![]() -3=
-3=![]() .若以D、E、P、Q为顶点的四边形是平行四边形,因为DE∥PQ,只须DE=PQ,设点P的坐标是(m,-m+4),则点Q的坐标是(m,-
.若以D、E、P、Q为顶点的四边形是平行四边形,因为DE∥PQ,只须DE=PQ,设点P的坐标是(m,-m+4),则点Q的坐标是(m,-![]() m2+m+4).分两种情况进行讨论:①当0<m<4时,PQ=(-
m2+m+4).分两种情况进行讨论:①当0<m<4时,PQ=(-![]() m2+m+4)-(-m+4)=-
m2+m+4)-(-m+4)=-![]() m2+2m,解方程-
m2+2m,解方程-![]() m2+2m=
m2+2m=![]() ,求出m的值,得到P1(3,1);②当m<0或m>4时,PQ=(-m+4)-(-
,求出m的值,得到P1(3,1);②当m<0或m>4时,PQ=(-m+4)-(-![]() m2+m+4)=
m2+m+4)=![]() m2-2m,解方程
m2-2m,解方程![]() m2-2m=
m2-2m=![]() ,求出m的值,得到P2(2+
,求出m的值,得到P2(2+![]() ,2-
,2-![]() ),P3(2-
),P3(2-![]() ,2+
,2+![]() ).
).
试题解析:(1)由抛物线经过点C(O,4)可得c=4,①
∵对称轴x=![]() =1,∴b=-2a,②,
=1,∴b=-2a,②,
又抛物线过点A(一2,O)∴0=4a-2b+c,③
由①②③ 解得:a=![]() , b=1 ,c=4.
, b=1 ,c=4.
所以抛物线的解析式是![]()
(2)假设存在满足条件的点F,连接BF、CF、OF.
过点F分别作FH⊥x轴于H , FG⊥y轴于G.
设点F的坐标为(t, ![]()
![]() +t+4),其中O<t<4, 则FH=
+t+4),其中O<t<4, 则FH=![]()
![]() +t+4 FG=t,
+t+4 FG=t,
∴![]() =
=![]() OB.FH=
OB.FH=![]() ×4×(
×4×(![]()
![]() +4t+4)=-
+4t+4)=-![]() +2t+8 ,
+2t+8 ,
![]() =
=![]() OC.FC=
OC.FC=![]() ×4×t=2t
×4×t=2t
![]()
令-![]() +4t+12 =17,即
+4t+12 =17,即![]() -4t+5=0,则△= -4<0,
-4t+5=0,则△= -4<0,
∴方程![]() -4t+5=0无解,故不存在满足条件的点F.
-4t+5=0无解,故不存在满足条件的点F.
(3)设直线BC的解析式为y=kx+b(k≠O),又过点B(4,0), C(0,4)
所以![]() ,解得:
,解得:![]() ,
,
所以直线BC的解析式是y= -x+4.
由y=![]()
![]() +4x+4=
+4x+4=![]()
![]() +
+![]() ,得D(1,
,得D(1,![]() ),
),
又点E在直线BC上,则点E(1,3),
于是DE=![]() -3=
-3= ![]() .
.
若以D.E.P.Q为顶点的四边形是平行四边形,
因为DE∥PQ,只须DE=PQ,
设点P的坐标是(m,-m+4),则点Q的坐标是(m,-![]()
![]() +m+4).
+m+4).
①当O<m<4时,PQ=(-![]()
![]() +m+4)-(-m+4)= -
+m+4)-(-m+4)= -![]()
![]() +2m.
+2m.
由-![]()
![]() +2m=
+2m=![]() ,解得:m=1或3.
,解得:m=1或3.
当m=1时,线段PQ与DE重合,m=-1舍去,
∴m=-3,此时P1 (3,1).
②当m<0或m>4时,PQ=(-m+4)-(-![]()
![]() ++m+4)=
++m+4)= ![]()
![]() -2m,
-2m,
由![]()
![]() -2m=
-2m=![]() ,解得m=2±
,解得m=2±![]() ,经检验适合题意,
,经检验适合题意,
此时P2(2+![]() ,2-
,2-![]() ),P3(2-
),P3(2-![]() ,2+
,2+![]() ).
).
综上所述,满足条件的点P有三个,分别是P1 (3,1),P2(2+![]() ,2 -
,2 -![]() ),P3(2-
),P3(2-![]() ,2+
,2+![]() )
)


科目:初中数学 来源: 题型:
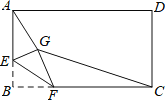
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为改善办学条件,计划购进![]() 两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
A | 240 | 0 | 210 | 20 |
B | 300 | 0 | 250 | 30 |
(Ⅰ)如果在线下购买![]() 两种书架20个,共花费5520元,求
两种书架20个,共花费5520元,求![]() 两种书架各购买了多少个;
两种书架各购买了多少个;
(Ⅱ)如果在线上购买![]() 两种书架20个,共花费
两种书架20个,共花费![]() 元,设其中
元,设其中![]() 种书架购买
种书架购买![]() 个,求W关于
个,求W关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)在(Ⅱ)的条件下,若购买![]() 种书架的数量不少于
种书架的数量不少于![]() 种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.
种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,
设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)

(1)填空:EF= .cm,GH= .cm;(用含x的代数式表示)
(2)若折成的长方体盒子的表面积为950cm2,求该长方体盒子的体积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价y1(元/台)与采购数量x1(台)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).
(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的![]() ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?
(2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润
查看答案和解析>>
科目:初中数学 来源: 题型:
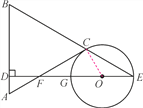
【题目】如图,△ABC中,AB=AC,点E是线段BC延长线上一点,ED⊥AB,垂足为D,ED交线段AC于点F,点O在线段EF上,⊙O经过C、E两点,交ED于点G.
(1)求证:AC是⊙O的切线;
(2)若∠E=30°,AD=1,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
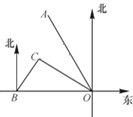
【题目】如图所示,港口B位于港口O正西方向120 km处,小岛C位于港口O北偏西60°的方向.一艘游船从港口O出发,沿OA方向(北偏西30°)以v km/h的速度驶离港口O,同时一艘快艇从港口B出发,沿北偏东30°的方向以60 km/h的速度驶向小岛C,在小岛C用1 h加装补给物资后,立即按原来的速度给游船送去.
(1)快艇从港口B到小岛C需要多长时间?
(2)若快艇从小岛C到与游船相遇恰好用时1h,求v的值及相遇处与港口O的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA
与⊙O的另一个交点为E,连结AC,CE。

(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com