练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】二次函数的部分图象如图，图象过点（﹣1，0），对称轴为直线，下列结论：①；②；③；④当时， 随的增大而增大．其中正确的结论有（　　 ）

    A. 1个 B. 2个 C. 3个 D. 4个

    【答案】B

    【解析】试题分析：根据抛物线的对称轴为直线x=﹣=2，则有4a+b=0故①正确；

    观察函数图象得到当x=﹣3时，函数值y＜0，则9a﹣3b+c＜0，即9a+c＜3b，故②错误；

    由于x=﹣1时，y=0，则a﹣b+c=0，易得c=﹣5a，所以8a+7b+2c=8a﹣28a﹣10a=﹣30a，再根据抛物线开口向下得a＜0，于是有8a+7b+2c＞0，故③正确；

    由于对称轴为直线x=2，根据二次函数的性质得到当x＞2时，y随x的增大而减小，故④错误．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】平面内的两条直线有相交和平行两种位置关系

    （1）如图a，若AB∥CD，点P在AB、CD外部，则有∠B＝∠BOD，又因∠BOD是△POD的外角，故∠BOD＝∠BPD+∠D，得∠BPD＝∠B﹣∠D．将点P移到AB、CD内部，如图b，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何数量关系？请证明你的结论；

    （2）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则∠BPD、∠B、∠D、∠BQD之间有何数量关系？（不需证明）

    （3）根据（2）的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修．技术工人骑摩托车先走，15分钟后，抢修车装载着所需材料出发，结果他们同时到达．已知抢修车的速度是摩托车的1.5倍，求这两种车的速度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠MAN=120°，AC平分∠MAN．

    （1）在图1中，若∠ABC=∠ADC=90°，求证：AB+AD=AC；

    （2）在图2中，若∠ABC+∠ADC=180°，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】魔术大师夏尔巴比耶90岁时定义了一个魔法三角阵，三角阵中含有四个区域（三个“边区域”和一个“核心区域”，如图1中的阴影部分），每个区域都含有5个数，把差相同的连续九个正整数填进三角阵中，每个区域的5个数的和必须相同。例如：图2中，把相差为1的九个数（1至9）填入后，三个“边区域”及“核心区域”的数的和都是22，即6+1+9+2+4=22，4+2+8+3+5=22，5+3+7+1+6=22，2+9+1+7+3=22

    （1）操作与发现：

    在图3中，小明把差为1的连续九个正整数（1至9）分为三组，其中1、2、3为同一组，4、5、6为同一组，7、8、9为同一组，把同组数填进同一花纹的△中，生成了一个符合定义的魔法三角阵，且各区域的5个数的和为28，请你在图3中把小明的发现填写完整.

    （2）操作与应用：

    根据（1）发现的结果，把差为8的连续九个正整数填进图4中，仍能得到符合定义的魔法三角阵，且各区域的5个数的和为2019.

    ①设其中最小的数为，则最大的数是_________;（用含的式子表示）.

    ②把图4中的9个数填写完整，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

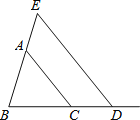
    【题目】如图，已知△ABC．

    （1）若AB=4，AC=5，则BC边的取值范围是　　；

    （2）点D为BC延长线上一点，过点D作DE∥AC，交BA的延长线于点E，若∠E=55°，∠ACD=125°，求∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，一蚂蚁从A点出发，沿着A→B→C→D→A…循环爬行，其中A点的坐标为（2，﹣2），B点的坐标为（﹣2，﹣2），C点的坐标为（﹣2，6），D点的坐标为（2，6），当蚂蚁爬了2018个单位时，蚂蚁所处位置的坐标为（　　）

    A. （﹣2，0）B. （4，﹣2）C. （﹣2，4）D. （0，﹣2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数的图象经过， 两点.

    （1）求对应的函数表达式；

    （2）将先向左平移1个单位，再向上平移4个单位，得到抛物线，将对应的函数表达式记为，求对应的函数表达式；

    （3）设，在（2）的条件下，如果在≤x≤a内存在某一个x的值，使得≤成立，根据函数图象直接写出a的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

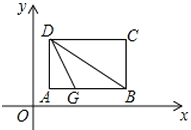
    【题目】如图，把矩形纸片ABCD置于直角坐标系中，AB∥x轴，BC∥y轴，AB=4，BC=3，点B（5，1）翻折矩形纸片使点A落在对角线DB上的H处得折痕DG．

    （1）求AG的长；

    （2）在坐标平面内存在点M（m，-1）使AM+CM最小，求出这个最小值；

    （3）求线段GH所在直线的解析式．

    查看答案和解析>>

    同步练习册答案