练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数的图象经过， 两点.

    （1）求对应的函数表达式；

    （2）将先向左平移1个单位，再向上平移4个单位，得到抛物线，将对应的函数表达式记为，求对应的函数表达式；

    （3）设，在（2）的条件下，如果在≤x≤a内存在某一个x的值，使得≤成立，根据函数图象直接写出a的取值范围.

    【答案】（1）；（2）；（3）a≥.

    【解析】试题分析：（1）根据待定系数法，可得函数解析式；

    （2）根据抛物线平移的规律：向左平移加，向上平移加，可得答案；

    （3）根据函数与不等式的关系，可得答案．

    试题解析：解：（1）∵二次函数的图象经过， 两点，∴，解得，∴抛物线的函数表达式为；

    （2）∵，∴抛物线的顶点为，∴平移后抛物线的顶点为，它对应的函数表达式为；

    （3）（见图）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中,，AD平分∠CAB，交CB于点D，过点D作于点E．若，CD=5，．

    （1）求BD的长

    （2）AE与BE相等吗？说明理由。

    （3）求△ABC的面积

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数的部分图象如图，图象过点（﹣1，0），对称轴为直线，下列结论：①；②；③；④当时， 随的增大而增大．其中正确的结论有（　　 ）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

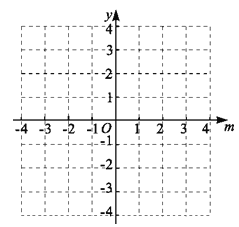
    【题目】已知：关于x的一元二次方程mx2﹣（4m+1）x+3m+3=0 （m＞1）.

    （1）求证：方程有两个不相等的实数根；

    （2）设方程的两个实数根分别为x1，x2（其中x1＞x2），若y是关于m的函数，且y=x1﹣3x2，求这个函数的解析式；

    （3）将（2）中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当关于m的函数y=2m+b的图象与此图象有两个公共点时，b的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠ABC=90°，点D，F分别是AC，AB的中点，CE∥DB，BE∥DC．

    （1）求证：四边形DBEC是菱形；

    （2）若AD=3，DF=1，求四边形DBEC面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E的坐标分别为（3，0），（0，1）.

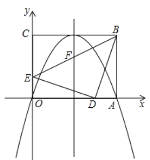
    （1）求抛物线的解析式；

    （2）猜想△EDB的形状并加以证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P是以O为圆心，AB为直径的半圆上的动点，AB=6cm，设弦AP的长为xcm，△APO的面积为ycm2，（当点P与点A或点B重合时，y的值为0）．小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整；

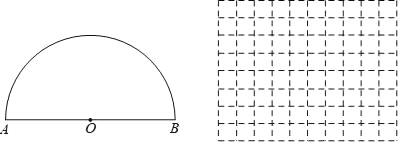
    （1）通过取点、画图、测量、计算，得到了x与y的几组值，如下表：

    x/cm

    0.5

    1

    2

    3

    3.5

    4

    5

    5.5

    5.8

    y/cm2

    0.8

    1.5

    2.8

    3.9

    4.2

    m

    4.2

    3.3

    2.3

    那么m=　 　；（保留一位小数）

    （2）建立平面直角坐标系，描出以表中各组对应值为坐标的点，画出该函数图象．

    （3）结合函数图象说明，当△APO的面积是4时，则AP的值约为　 　．（保留一位小数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某巡警骑摩托车在一条南北大道上巡逻，某天他从岗亭出发，晚上停留在处，规定向北方向为正，当天行驶纪录如下（单位：千米）

    ，，，，，，，

    在岗亭何方？距岗亭多远？

    在行驶过程中，最远处离出发点有多远？

    若摩托车行驶千米耗油升，这一天共耗油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

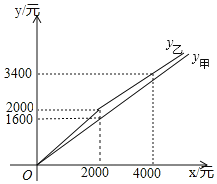
    【题目】长沙市的“口味小龙虾”冠绝海内外，如“文和友老长沙龙虾馆”订单排队上千号．某衣贸市场甲、乙两家农贸商店售卖小龙虾，甲、乙平时以同样的价格出售品质相同的小龙虾，“中非贸易博览会”期间，甲、乙两家商店都让利酬宾，付款金额y甲，y乙（单位：元）与原价x（单位：元）之间的函数关系如图所示．

    （1）请求出y甲，y乙关于x的函数关系式；

    （2）“中非贸易博览会”期间，如果你是龙虾馆采购员，如何选择甲、乙两家商店购买小龙虾更省钱？

    查看答案和解析>>

    同步练习册答案