
����Ŀ������ͣ��������ƴ����סլС��ͣ���ѵ����⣬��ͼ����ȪijС���ĵ���ͣ�����µ���ڵ����ʾ��ͼ�����У�AB��BD����BAD��18�㣬C��BD�ϣ�BC��0.5m�����ݹ涨������ͣ�����µ�����Ϸ�Ҫ�����߱�־���Ա��֪��ʻԱ���ݳ����ܷ�ȫʻ�룮С����ΪCD�ij����������Ƶĸ߶ȣ���С����ΪӦ����CE�ij���Ϊ���Ƶĸ߶ȣ�С�պ�С��˭˵�öԣ������жϲ��������ȷ�����Ƹ߶ȣ��������ȷ��0.1m���ο����ݣ�sin18���0.31��cos18���0.95��tan18���0.325��
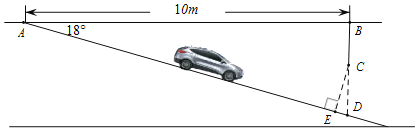
���𰸡�С��˵�Ķԣ�CEΪ2.6m��
��������
�ȸ���CE��AE,�жϳ�CEΪ��,�ٸ��ݽ�ֱ�������ε�֪ʶ���
�⣺�ڡ�ABD��,��ABD��90��,��BAD��18��,BA��10m,
��tan��BAD��![]() ��
��
��BD��10��tan18��,
��CD��BD��BC��10��tan18�㩁0.5��2.7��m��,
�ڡ�ABD��,��CDE��90�㩁��BAD��72��,
��CE��ED,
��sin��CDE��![]() ,
,
��CE��sin��CDE��CD��sin72���2.7��2.6��m��,
��2.6m��2.7m,��CE��AE,
��С��˵�Ķԣ�
��С��˵�Ķ�,CEΪ2.6m��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������������࣬���ҵ��չѸ�١�����ij��ݹ�˾������·���ʮ�·����Ͷ�ݵĿ���ܼ����ֱ�Ϊ![]() �����
�����![]() ������ٶ��ù�˾ÿ�µ�Ͷ���ܼ�������������ͬ.
������ٶ��ù�˾ÿ�µ�Ͷ���ܼ�������������ͬ.
��1����ÿ�ݹ�˾ÿ�µ�Ͷ���ܼ�������ƽ�������ʣ�
��2��������˫ʮһ��������������Ԥ��11����Ͷ�ݵĿ���ܼ����������ʽ���ԭ��![]() �������ÿ��ÿ������Ͷ�ݿ��
�������ÿ��ÿ������Ͷ�ݿ��![]() ������ù�˾����
������ù�˾����![]() ��ҵ��Ա���Ƿ�����ɵ���Ͷ������������ܣ�����ʱ��Ƹ����ҵ��Ա��
��ҵ��Ա���Ƿ�����ɵ���Ͷ������������ܣ�����ʱ��Ƹ����ҵ��Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����װ���������������ַ�װ��100�������ò��ó���7500Ԫ.���ַ�װÿ������80Ԫ��ÿ���ۼ�120Ԫ�����ַ�װÿ������60Ԫ��ÿ���ۼ�90Ԫ.
�����蹺�����ַ�װ![]() ��������д�±�.
����������.
��һ
�������ַ�װ������/�� | 10 | 20 | �� |
|
�������ַ�װ���÷���/Ԫ | 800 | 1600 | �� | |
�������ַ�װ���÷���/Ԫ | 5400 | �� |
����
�������ַ�װ������/�� | 10 | 20 | �� |
|
���ַ�װ��õ�����/Ԫ | 800 | �� | ||
���ַ�װ��õ�����/Ԫ | 2700 | 2400 | �� |
�������ܹ�����������Ľ�����������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB��BC����D��AC�ߵ��е㣬�ӳ�BD����E��ʹ��DE��BD������CE��
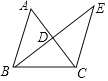
��1����֤����ABD�ա�CED��
��2����BC��5��CD��3ʱ�����BCE���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��3��BC��4����E��AB����һ�㣬��AE��2����F�DZ�BC�ϵ�����һ�㣬�ѡ�BEF��EF���ۣ���B�Ķ�Ӧ��ΪG������AG��CG�����ı���AGCD���������СֵΪ_____��
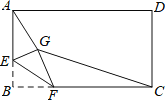
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ����ÿ��С�����εı߳�Ϊ1�������У���A����B����C�����ڸ����.
����ÿ��С�����εı߳�Ϊ1�������У���A����B����C�����ڸ����.
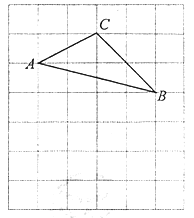
��I������![]() ��ֵ����____________��
��ֵ����____________��
����������ͼ��ʾ�������У����̶���ֱ�ߣ�����һ����ABΪһ�ߡ��������![]() �ľ��Σ�����Ҫ˵����ͼ��������Ҫ��֤����_____________.
�ľ��Σ�����Ҫ˵����ͼ��������Ҫ��֤����_____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м���������4����ͬ��С�������ɵģ���������ͼ������ͼ��ͬ���ǣ�������
A. B.
B.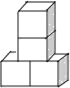 C.
C.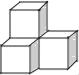 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��x�ύ��A��B���㣨��d�ڵ�B���Ҳࣩ����y�ύ�ڵ�
��x�ύ��A��B���㣨��d�ڵ�B���Ҳࣩ����y�ύ�ڵ�![]() ������ΪD.
������ΪD.
��I����������ߵĽ���ʽ������D�����꣺
����QΪ�߶�BD��һ�㣬��A���ڡ�AQB��ƽ���ߵĶԳƵ�ΪA'��
���жϵ�A'��ֱ��BQ��λ�ù�ϵ����![]() ����д���ڡ����ڡ���ֱ��BQ�ϣ�
����д���ڡ����ڡ���ֱ��BQ�ϣ�
����![]() �����2�����꣺
�����2�����꣺
�������������ߵĶԳ����ϵĵ�P����![]() �����P�����ꡣ
�����P�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̼Ҽƻ��ӳ��Ҳɹ��յ��ͱ������ֲ�Ʒ��20̨���յ��IJɹ�����y1��Ԫ/̨����ɹ�����x1��̨������y1=��20x1+1500��0��x1��20��x1Ϊ������������IJɹ�����y2��Ԫ/̨����ɹ�����x2��̨������y2=��10x2+1300��0��x2��20��x2Ϊ��������
��1�����̼��볧��Э�̣��ɹ��յ������������ڱ���������![]() ���ҿյ��ɹ����۲�����1200Ԫ���ʸ��̼ҹ��м��ֽ���������
���ҿյ��ɹ����۲�����1200Ԫ���ʸ��̼ҹ��м��ֽ���������
��2�����̼ҷֱ���1760Ԫ/̨��1700Ԫ/̨�����۵����۳��յ��ͱ��䣬��ȫ�����꣮�ڣ�1���������£��ʲɹ��յ�����̨ʱ������������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com