
【题目】如图,在等腰△ABC中,AB=BC,点D是AC边的中点,延长BD至点E,使得DE=BD,连结CE.
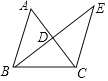
(1)求证:△ABD≌△CED.
(2)当BC=5,CD=3时,求△BCE的周长.
科目:初中数学 来源: 题型:
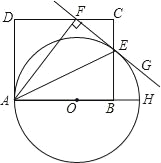
【题目】如图,AH是圆O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.
(1)求证:直线FG是⊙O的切线;
(2)若AD=8,EB=5,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
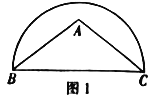
【题目】在![]() 中,
中,![]() ,点
,点![]() 在以
在以![]() 为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中作弦![]() ,使
,使![]() ;
;
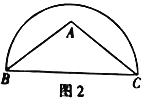
(2)在图2中以![]() 为边作一个45°的圆周角.
为边作一个45°的圆周角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(0,4)和(1,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A在直线y=![]() x﹣1上,则点B与点O′之间的距离为( )
x﹣1上,则点B与点O′之间的距离为( )
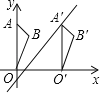
A.3B.4C.3![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=3,点E是边CD的中点,点P,Q分别是射线DC与射线EB上的动点,连结PQ,AP,BP,设DP=t,EQ=![]() t.
t.
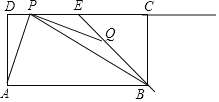
(1)当点P在线段DE上(不包括端点)时.
①求证:AP=PQ;②当AP平分∠DPB时,求△PBQ的面积.
(2)在点P,Q的运动过程中,是否存在这样的t,使得△PBQ为等腰三角形?若存在,请求出t的值;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地下停车场的设计大大缓解了住宅小区停车难的问题,如图是龙泉某小区的地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小刚认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小刚和小亮谁说得对?请你判断并计算出正确的限制高度.(结果精确到0.1m,参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.325)
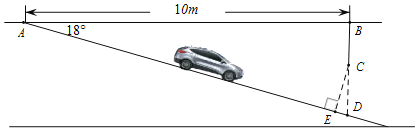
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在紧张的中考复习之际,为确保学生的饮食健康与安全,部分家长组织成立中考护卫小分队,每天不辞辛劳从城区进购正规检疫菜品。某甲、乙两种菜品每份进价分别为 14 元、16 元,售价均为每份 18 元,这两种菜品每天的进价总额为 1480 元,全部销售完每天总利润为 320 元.
(1)该甲、乙两种菜品每天各卖出多少份?
(2)因受气温变化的影响,甲种菜品进价每份上涨 a 0 a 4元,为确保学生的营养,在每天两种菜品的进购总量不变的情况下,要求甲种菜品的数量不得低于 10 份,也不超过乙种菜品的 3 倍,则进购甲种菜品多少份才能使每天的总利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com