
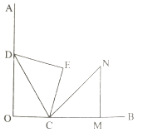
【题目】如图![]() ,
,![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 上,则
上,则![]() 值为()
值为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 | 乙 | 丙 | |
平均数 | 7.9 | 7.9 | 8.0 |
方差 | 3.29 | 0.49 | 1.8 |
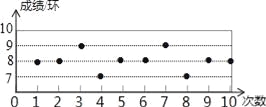
根据以上图表信息,参赛选手应选( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
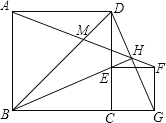
【题目】如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HEHB=4-2![]() ,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=
,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=![]() AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点A(-1,0),点B(-3,0),且OB=OC,
轴交于点A(-1,0),点B(-3,0),且OB=OC,
(1)求抛物线的解析式;
(2)点P在抛物线上,且∠POB=∠ACB,求点P的坐标;
(3)抛物线上两点M,N,点M的横坐标为m,点N的横坐标为m+4.点D是抛物线上M,N之间的动点,过点D作y轴的平行线交MN于点E.
①求DE的最大值.
②点D关于点E的对称点为F.当m为何值时,四边形MDNF为矩形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“网购”的增多,快递业务发展迅速。我市某快递公司今年八月份与十月份完成投递的快递总件数分别为![]() 万件和
万件和![]() 万件,假定该公司每月的投递总件数的增长率相同.
万件,假定该公司每月的投递总件数的增长率相同.
(1)求该快递公司每月的投递总件数的月平均增长率;
(2)由于“双十一”购买量激增,预计11月需投递的快递总件数的增长率将是原来![]() 倍,如果每人每月最多可投递快递
倍,如果每人每月最多可投递快递![]() 万件,该公司现有
万件,该公司现有![]() 名业务员,是否能完成当月投递任务?如果不能,需临时招聘几名业务员?
名业务员,是否能完成当月投递任务?如果不能,需临时招聘几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.

依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“一带一路”战略给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年人均收入人民币2600元,预计2018年人均收入将达到人民币13000元,设2016年到2018年该地区居民人均收入平均增长率为x,可列方程为( ).
A.2600(1+2x)=13000B.2600(1+x)2=13000
C.2600(1+x2)=13000D.2600+2x=13000
查看答案和解析>>
科目:初中数学 来源: 题型:
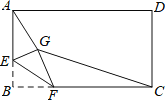
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com