
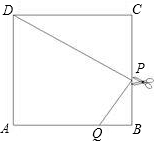
 如图,边长为3的正方形纸片ABCD,用剪刀沿PD剪下Rt△PCD,其中∠PDC=30°.
如图,边长为3的正方形纸片ABCD,用剪刀沿PD剪下Rt△PCD,其中∠PDC=30°.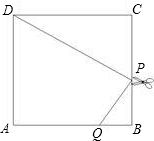 解:(1)法一:在Rt△PCD中,∠C=90°,∠PDC=30°,CD=3,
解:(1)法一:在Rt△PCD中,∠C=90°,∠PDC=30°,CD=3,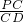 ,
, =
= .
.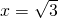 (舍去负值),
(舍去负值), .
. .
. ,
,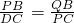 时,△PBQ∽△DCP,
时,△PBQ∽△DCP,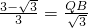 ,
, -1,
-1, -1,时,△PBQ∽△DCP.
-1,时,△PBQ∽△DCP. .
. ,
, ,可得
,可得 )×
)× =
= -1,
-1, -1时,△PBQ∽△DCP.
-1时,△PBQ∽△DCP. ;
; -1时,△PBQ∽△DCP.
-1时,△PBQ∽△DCP.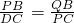 时△PBQ∽△DCP,可求出QB.
时△PBQ∽△DCP,可求出QB. ,可得BP,要使△PBQ∽△DCP,则必须有∠BPQ=∠CDP=30°再由tan∠BPQ=
,可得BP,要使△PBQ∽△DCP,则必须有∠BPQ=∠CDP=30°再由tan∠BPQ= 可求得QB.
可求得QB.

科目:初中数学 来源: 题型:
 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.查看答案和解析>>
科目:初中数学 来源:2012-2013学年新人教版九年级(上)期中数学试卷(7)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com