
【题目】已知:如图,Rt△ABC中,∠BAC=90 ![]() ,AB=AC,D是BC的中点,AE=BF.
,AB=AC,D是BC的中点,AE=BF.
求证:
(1)DE =DF;
(2)若BC =8,求四边形AFDE的面积.
【答案】
(1)证明:如图,连AD,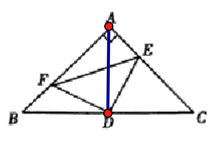
![]() 中,
中, ![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
在△DAE和△DBF中, 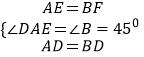 ,
,
∴△DAE≌△DBF ![]()
∴DE=DF
(2)证明:∵BC=8,
∴AD= ![]() BC=4
BC=4
∵△DAE≌△DBF,
∴四边形AFDE的面积= ![]() =
= ![]()
【解析】(1)连AD,根据等腰直角三角形的性质得出∠ B = ∠ C = 45 , 根据等腰三角形的三线合一得出∠ DAE = ∠ BAD = 45 ,进而得到∠ BAD = ∠ B = 45 ,然后利用SAS判断出△DAE≌△DBF ( SAS ) ,由全等三角形的对应边相等得出DE=DF ;
(2)根据直角三角形斜边上的中线等于斜边的一半得出AD的长度,然后由全等三角形的面积相等得出四边形AFDE的面积= S ΔABD就可以算出结果了。


科目:初中数学 来源: 题型:
【题目】阅读理解
∵ ![]() <
< ![]() <
< ![]() ,即2<
,即2< ![]() <3.
<3.
∴1< ![]() ﹣1<2
﹣1<2
∴ ![]() ﹣1的整数部分为1.
﹣1的整数部分为1.
∴ ![]() ﹣1的小数部分为
﹣1的小数部分为 ![]() ﹣2.
﹣2.
解决问题:
已知a是 ![]() ﹣3的整数部分,b是
﹣3的整数部分,b是 ![]() ﹣3的小数部分,求(﹣a)3+(b+4)2的平方根.
﹣3的小数部分,求(﹣a)3+(b+4)2的平方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球(除颜色外其余都相同),其中红球有2个,黑球有1个,绿球有3个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E,∠ABC的平分线BF交CD于点F,过点A作AH⊥CD于H,当EDC=30 ![]() ,CF=
,CF= ![]() ,则DH= .
,则DH= . 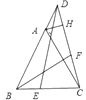
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“武夷水秀”以特有的光影效果,吸引众多市民前去观看.特别是五一当天,共演了7场,平均每场有1200人观看,这天观看的总人数用科学记数法可以表示为( )
A.0.12×104
B.1.2×103
C.8.4×103
D.84×102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( ) 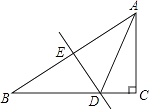
A.6
B.6 ![]()
C.9
D.3 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com