
【题目】如图,四边形![]() 为菱形,以
为菱形,以![]() 为直径作
为直径作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 是
是![]() 上的一点,且
上的一点,且![]() ,连接
,连接![]() .
.
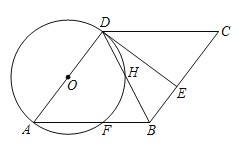
(1)求证:![]() .
.
(2)求证:![]() 是
是![]() 的切线.
的切线.
(3)若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,并与
,并与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是对称轴与
是对称轴与![]() 轴的交点.
轴的交点.
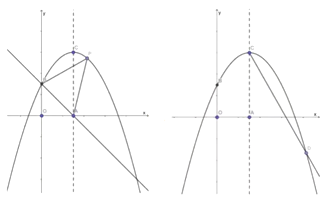
(1)求抛物线的解析式;
(2)如图①所示, ![]() 是抛物线上的一个动点,且位于第一象限,连结BP、AP,求
是抛物线上的一个动点,且位于第一象限,连结BP、AP,求![]() 的面积的最大值;
的面积的最大值;
(3)如图②所示,在对称轴![]() 的右侧作
的右侧作![]() 交抛物线于点
交抛物线于点![]() ,求出
,求出![]() 点的坐标;并探究:在
点的坐标;并探究:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
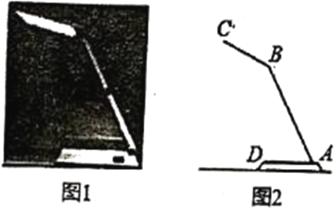
【题目】如图1是一种折叠台灯,将其放置在水平桌面上,图2是其简化示意图,测得其灯臂![]() 长为
长为![]() 灯翠
灯翠![]() 长为
长为![]() ,底座
,底座![]() 厚度为
厚度为![]() 根据使用习惯,灯臂
根据使用习惯,灯臂![]() 的倾斜角
的倾斜角![]() 固定为
固定为![]() ,
,
(1)当![]() 转动到与桌面平行时,求点
转动到与桌面平行时,求点![]() 到桌面的距离;
到桌面的距离;
(2)在使用过程中发现,当![]() 转到至
转到至![]() 时,光线效果最好,求此时灯罩顶端
时,光线效果最好,求此时灯罩顶端![]() 到桌面的高度(参考数据:
到桌面的高度(参考数据:![]() ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=2![]() AB.将矩形ABCD对折,得到折痕MN,沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②AB=
AB.将矩形ABCD对折,得到折痕MN,沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②AB=![]() BP;③PN=PG;④PM=PF;⑤若连接PE,则△PEG∽△CMD.其中正确的个数为( )
BP;③PN=PG;④PM=PF;⑤若连接PE,则△PEG∽△CMD.其中正确的个数为( )
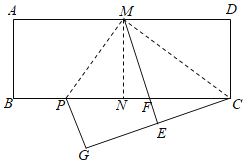
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E为AB上的一点,EF⊥AB,交BD于点F.
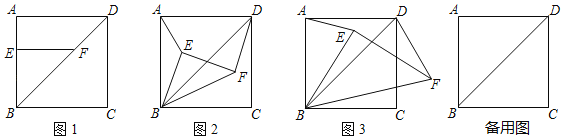
(1)如图1,直按写出![]() 的值 ;
的值 ;
(2)将△EBF绕点B顺时针旋转到如图2所示的位置,连接AE、DF,猜想DF与AE的数量关系,并证明你的结论;
(3)如图3,当BE=BA时,其他条件不变,△EBF绕点B顺时针旋转,设旋转角为α(0°<α<360°),当α为何值时,EA=ED?在图3或备用图中画出图形,并直接写出此时α= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.该函数的图象的开口向下B.该函数图象的顶点坐标是![]()
C.当![]() 时,
时,![]() 随
随![]() 的增大而增大D.该函数的图象与
的增大而增大D.该函数的图象与![]() 轴有两个不同的交点
轴有两个不同的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为![]() ,为保护廊桥的安全,在该抛物线上距水面
,为保护廊桥的安全,在该抛物线上距水面![]() 高为8米的点
高为8米的点![]() 、
、![]() 处要安装两盏警示灯,则这两盏灯的水平距离
处要安装两盏警示灯,则这两盏灯的水平距离![]() 是____米.
是____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
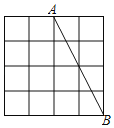
【题目】如图,正方形网格中,每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上,请按要求画出图形并计算.
(1)以线段AB为一腰的等腰△ABC,点C在小正方形的顶点上,且S△ABC=6;
(2)以BC为对角线作平行四边形BDCE,点D,E均在小正方形的顶点上,且∠ABD=45°;
(3)连接DE,请直接写出线段DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com