
【题目】在平面直角坐标系中,二次函数y=ax2+![]() x+c的图象经过点C(0,2)和点D(4,﹣2).点E是直线y=﹣
x+c的图象经过点C(0,2)和点D(4,﹣2).点E是直线y=﹣![]() x+2与二次函数图象在第一象限内的交点.
x+2与二次函数图象在第一象限内的交点.
(1)求二次函数的解析式及点E的坐标.
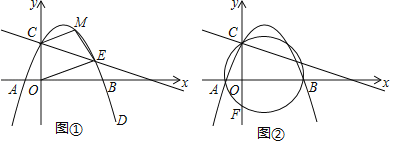
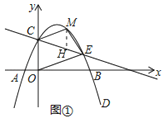
(2)如图①,若点M是二次函数图象上的点,且在直线CE的上方,连接MC,OE,ME.求四边形COEM面积的最大值及此时点M的坐标.
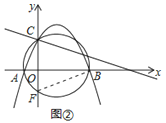
(3)如图②,经过A、B、C三点的圆交y轴于点F,求点F的坐标.
【答案】(1)E(3,1);(2)S最大=![]() ,M坐标为(
,M坐标为(![]() ,3);(3)F坐标为(0,﹣
,3);(3)F坐标为(0,﹣![]() ).
).
【解析】
1)把C与D坐标代入二次函数解析式求出a与c的值,确定出二次函数解析式,与一次函数解析式联立求出E坐标即可;
(2)过M作MH垂直于x轴,与直线CE交于点H,四边形COEM面积最大即为三角形CME面积最大,构造出二次函数求出最大值,并求出此时M坐标即可;
(3)令y=0,求出x的值,得出A与B坐标,由圆周角定理及相似的性质得到三角形AOC与三角形BOF相似,由相似得比例求出OF的长,即可确定出F坐标.
(1)把C(0,2),D(4,﹣2)代入二次函数解析式得: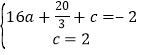 ,
,
解得: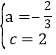 ,即二次函数解析式为y=﹣
,即二次函数解析式为y=﹣![]() x2+
x2+![]() x+2,
x+2,
联立一次函数解析式得: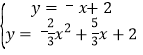 ,
,
消去y得:﹣![]() x+2=﹣
x+2=﹣![]() x2+
x2+![]() x+2,
x+2,
解得:x=0或x=3,
则E(3,1);
(2)如图①,过M作MH∥y轴,交CE于点H,
设M(m,﹣![]() m2+
m2+![]() m+2),则H(m,﹣
m+2),则H(m,﹣![]() m+2),
m+2),
∴MH=(﹣![]() m2+
m2+![]() m+2)﹣(﹣
m+2)﹣(﹣![]() m+2)=﹣
m+2)=﹣![]() m2+2m,
m2+2m,
S四边形COEM=S△OCE+S△CME=![]() ×2×3+
×2×3+![]() MH3=﹣m2+3m+3,
MH3=﹣m2+3m+3,
当m=﹣![]() =
=![]() 时,S最大=
时,S最大=![]() ,此时M坐标为(
,此时M坐标为(![]() ,3);
,3);
(3)连接BF,如图②所示,
当﹣![]() x2+
x2+![]() x+20=0时,x1=
x+20=0时,x1=![]() ,x2=
,x2=![]() ,
,
∴OA=![]() ,OB=
,OB=![]() ,
,
∵∠ACO=∠ABF,∠AOC=∠FOB,
∴△AOC∽△FOB,
∴![]() ,即
,即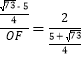 ,
,
解得:OF=![]() ,
,
则F坐标为(0,﹣![]() ).
).


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
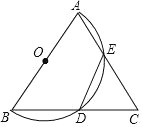
【题目】如图,已知△ABC 中,AB 为半圆 O 的直径,AC、BC 分别交半圆 O 于点 E、D,且 BD=DE.
(1)求证:点 D 是 BC 的中点.
(2)若点 E 是 AC 的中点,判断△ABC 的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A厂一月份产值为16万元,因管理不善,二、三月份产值的月平均下降率为x(0<x<1).B厂一月份产值为12万元,二月份产值下降率为x,经过技术革新,三月份产值增长,增长率为2x.三月份A、B两厂产值分别为yA、yB(单位:万元).
(1)分别写出yA、yB与x的函数表达式;
(2)当yA=yB时,求x的值;
(3)当x为何值时,三月份A、B两厂产值的差距最大?最大值是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
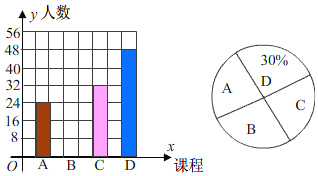
【题目】为深化课程改革,某校为学生开设了形式多样的社团课程,为了解部分社团课程在学生中最受欢迎的程度,学校随机抽取七年级部分学生进行调查,从A:文学签赏,B:科学探究,C:文史天地,D:趣味数学四门课程中选出你喜欢的课程(被调查者限选一项),并将调查结果绘制成两个不完整的统计图,如图所示,根据以上信息,解答下列问题:
(1)本次调查的总人数为多少人,扇形统计图中A部分的圆心角是多少度.
(2)请补全条形统计图.
(3)根据本次调查,该校七年级840名学生中,估计最喜欢“科学探究”的学生人数为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
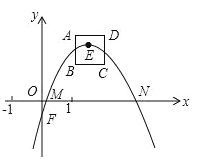
【题目】如图,抛物线l:y=﹣x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1).
(1)直接写出点D的坐标_____________;
(2)若l经过点B,C,求l的解析式;
(3)设l与x轴交于点M,N,当l的顶点E与点D重合时,求线段MN的值;当顶点E在正方形ABCD内或边上时,直接写出线段MN的取值范围;
(4)若l经过正方形ABCD的两个顶点,直接写出所有符合条件的c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在玩转盘游戏时,把两个可以自由转动的转盘A、B分成4等份、3等份的扇形区域,并在每一小区域内标上数字(如图所示),指针的位置固定.游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为3的倍数,甲胜;若指针所指两个区域的数字之和为4的倍数时,乙胜.如果指针落在分割线上,则需要重新转动转盘.

(1)试用列表或画树形图的方法,求甲获胜的概率;
(2)请问这个游戏规则对甲、乙双方公平吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com