
【题目】如图,已知△ABC 中,AB 为半圆 O 的直径,AC、BC 分别交半圆 O 于点 E、D,且 BD=DE.
(1)求证:点 D 是 BC 的中点.
(2)若点 E 是 AC 的中点,判断△ABC 的形状,并说明理由.
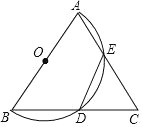
【答案】(1)详见解析;(2)△ABC是等边三角形.
【解析】
(1)连接AD,根据圆周角定理得到∠ADB=∠ADC=90°,证明△BAD≌△CAD,根据全等三角形的性质证明;
(2)根据直角三角形的性质得到DE=AE=EC,得到CA=CB,根据等边三角形的判定定理证明.
(1)连接AD,
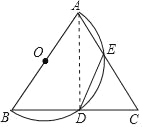
∵AB为半圆O的直径,
∴∠ADB=∠ADC=90°,
∵BD=DE,
∴![]() ,
,
∴∠BAD=∠CAD,
在△BAD和△CAD中,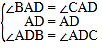 ,
,
∴△BAD≌△CAD(ASA),
∴BD=DC,即点D是BC的中点;
(2)∵△BAD≌△CAD,
∴AB=AC,
∵∠ADC=90°,点E是AC的中点,
∴DE=AE=EC,
由(1)得,DE=BD=DC,
∴CA=CB,
∴CA=CB=AB,
∴△ABC是等边三角形.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
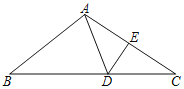
【题目】如图,△ABC的周长为30cm,把△ABC的边AC对折,使顶点A和C重合,折痕交BC边于点D,交AC边于点E,若△ABD的周长是22cm,则AE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
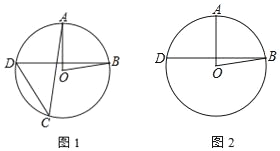
【题目】如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°
(1)若点C在优弧BD上,求∠ACD的大小;
(2)若点C在劣弧BD上,直接写出∠ACD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧![]() 于点P,Q,且点P, Q在AB异侧,连接OP.
于点P,Q,且点P, Q在AB异侧,连接OP.
(1)求证:AP=BQ;
(2)当BQ=4![]() 时,求扇形COQ的面积及
时,求扇形COQ的面积及![]() 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,请直接写出OC的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是课本中“作一个角等于已知角”的尺规作图过程.已知:∠AOB. 求作:一个角,使它等于∠AOB.作法:如图
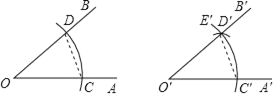
(1)作射线O'A';
(2)以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
(3)以O'为圆心,OC为半径作弧C'E',交O'A'于C';
(4)以C'为圆心,CD为半径作弧,交弧C'E'于D';
(5)过点D'作射线O'B'.
则∠A'O'B'就是所求作的角.
请回答:该作图的依据是( )
A.SSSB.SASC.ASAD.AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+4x与x轴的另一个交点为A,现将抛物线向右平移m(m>2)个单位长度,所得抛物线与x轴交于C,D,与原抛物线交于点P,设△PCD的面积为S,则用m表示S正确的是( )

A. ![]() (m2﹣4) B.
(m2﹣4) B. ![]() m2﹣2 C.
m2﹣2 C. ![]() (4﹣m2) D. 2﹣
(4﹣m2) D. 2﹣![]() m2
m2
查看答案和解析>>
科目:初中数学 来源: 题型:
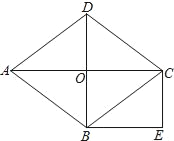
【题目】如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
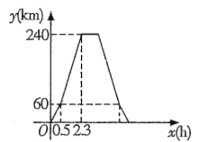
【题目】一辆快递车从长春出发,走高速公路,途经伊通,前往靖宇镇送快递,到达后卸货和休息共用![]() ,然后开车按原速原路返回长春.这辆快递车在长春到伊通、伊通到靖宇的路段上分别以不同的速度保持匀速前进,返回时也分别按原速返回.这辆快递车距离长春的路程
,然后开车按原速原路返回长春.这辆快递车在长春到伊通、伊通到靖宇的路段上分别以不同的速度保持匀速前进,返回时也分别按原速返回.这辆快递车距离长春的路程![]() 与它行驶的时间
与它行驶的时间![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)快递车从伊通到长春的速度是__________![]() ,快递车从长春到靖宇镇往返一共用了__________
,快递车从长春到靖宇镇往返一共用了__________![]() ;
;
(2)当这辆快递车在靖宇到伊通的路段上行驶时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)如果这辆快递车两次经过同一个服务区的时间间隔为![]() ,直接写出这个服务区距离伊通的路程.
,直接写出这个服务区距离伊通的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com