
【题目】如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为 
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=AC,则有BC边上的中线,高线和∠BAC的平分线重合于AD(如图一).若将等腰△ABC的顶点A向右平行移动后,得到△A′BC(如图二),那么,此时BC边上的中线、BC边上的高线和∠BA′C的平分线应依次分别是 , , .(填A′D、A′E、A′F)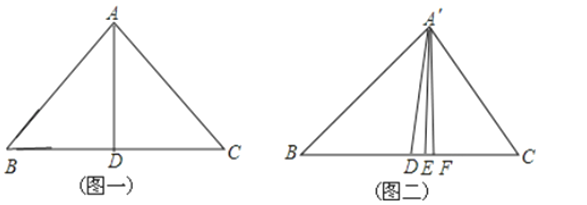
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程. 如图:在四边形ABCD中,∠A=106°﹣α,∠ABC=74°+α,BD⊥DC于点D,EF⊥DC于点F,求证:∠1=∠2
证明:∵∠A=106°﹣α,∠ABC=74°+α(已知)
∴∠A+∠ABC=180°
∴AD∥()
∴∠1=()
∵BD⊥DC,EF⊥DC(已知)
∴∠BDF=∠EFC=90°()
∴BD∥()
∴∠2=()
∴∠1=∠2()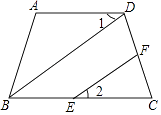
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.(1)求证:△ABD∽△AEB;(2)当![]() 时,求tanE;
时,求tanE;
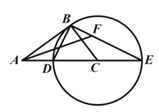
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的解析式为( ).
A.y=x+2
B.y=-x+2
C.y=x+2或y=-x+2
D.y=-x+2或y=x-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,对角线AC、BD交于点O , 点E是BC的中点 . 若OE=3cm , 则AB的长为( )
A.3cm
B.6cm
C.9cm
D.12cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com