
【题目】完成下面推理过程. 如图:在四边形ABCD中,∠A=106°﹣α,∠ABC=74°+α,BD⊥DC于点D,EF⊥DC于点F,求证:∠1=∠2
证明:∵∠A=106°﹣α,∠ABC=74°+α(已知)
∴∠A+∠ABC=180°
∴AD∥()
∴∠1=()
∵BD⊥DC,EF⊥DC(已知)
∴∠BDF=∠EFC=90°()
∴BD∥()
∴∠2=()
∴∠1=∠2()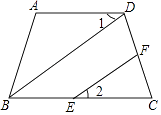
【答案】BC;同旁内角互补,两直线平行;∠DBC;两直线平行,内错角相等;垂直的定义;EF;同位角相等,两直线平行;∠DBC;两直线平行,同位角相等;等量代换
【解析】证明:∵∠A=106°﹣α,∠ABC=74°+α(已知), ∴∠A+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠1=∠DBC(两直线平行,内错角相等 ),
∵BD⊥DC,EF⊥DC(已知),
∴∠BDF=∠EFC=90°(垂直的定义),
∴BD∥EF(同位角相等,两直线平行),
∴∠2=∠DBC(两直线平行,同位角相等),
∴∠1=∠2(等量代换),
所以答案是:BC,同旁内角互补,两直线平行,∠DBC,垂直的定义,EF,同位角相等,两直线平行,∠DBC,两直线平行,同位角相等,等量代换.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列图形都是由边长为“1”的小正方形按一定规律组成,其中第1个图形有9个边长为1的小正方形,第2个图形有14个边长为1的小正方形…则第10个图形中边长为1的小正方形的个数为( )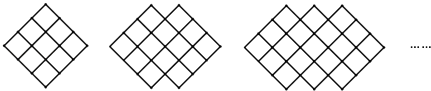
A.72
B.64
C.54
D.50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC的三个顶点的横坐标乘以﹣1,纵坐标不变,则所得图形( )
A. 与原图形关于y轴对称
B. 与原图形关于x轴对称
C. 与原图形关于原点对称
D. 向x轴的负方向平移了一个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com