
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以线段
,以线段![]() 为边在第四象限内作等边三角形
为边在第四象限内作等边三角形![]() ,点
,点![]() 为
为![]() 正半轴上一动点
正半轴上一动点![]() , 连接
, 连接![]() ,以线段
,以线段![]() 为边在第四象限内作等边三角形
为边在第四象限内作等边三角形![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 轴于点
轴于点![]() .
.
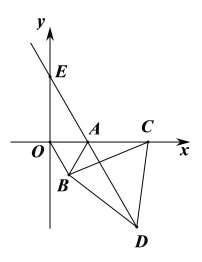
(1)求证:![]() ≌
≌![]() ;
;
(2)在点![]() 的运动过程中,
的运动过程中,![]() 的度数是否会变化?如果不变,请求出
的度数是否会变化?如果不变,请求出![]() 的度数;如果变化,请说明理由.
的度数;如果变化,请说明理由.
(3)当点![]() 运动到什么位置时,以
运动到什么位置时,以![]() 为顶点的三角形是等腰三角形?
为顶点的三角形是等腰三角形?
【答案】![]() 详见解析;
详见解析;![]() 的度数不会变化,
的度数不会变化,![]() ;
;![]() 当点
当点![]() 运动到
运动到![]() 时.
时.
【解析】
(1)根据等边三角形的性质可得BO=BA,BC=BD,∠OBA=∠CBD=60°,进而可利用SAS证明![]() ≌
≌![]() ;
;
(2)设BC、DE交于点F,如图1,根据全等三角形的性质可得∠1=∠2,根据三角形的内角和定理可得∠CAD=∠CBD,进而可得结论;
(3)易求得∠EAC=120°,∠OEA=30°,即得以A,E,C为顶点的三角形是等腰三角形时,AE和AC是腰,然后根据30°角的直角三角形的性质可得AE的长,进而可得AC、OC的长,即可得出点C的位置.
解:(1)证明:∵△AOB、△BCD是等边三角形,
∴BO=BA,BC=BD,∠OBA=∠CBD=60°,
∴∠OBC=∠ABD,
∴![]() ≌
≌![]() (SAS);
(SAS);
(2)设BC、DE交于点F,如图1,
∵![]() ≌
≌![]() ,∴∠1=∠2,
,∴∠1=∠2,
∵∠AFC=∠BFD,∴∠CAD=∠CBD=60°,
∴![]() 的度数不会变化,且
的度数不会变化,且![]() ;
;

(3)∵![]() ,∴∠EAC=120°,∠OAE=60°,∴∠OEA=30°,
,∴∠EAC=120°,∠OAE=60°,∴∠OEA=30°,
∴以A,E,C为顶点的三角形是等腰三角形时,AE和AC是腰,
∵在Rt△AOE中,OA=1,∠OEA=30°,∴AE=2,
∴AC=AE=2,∴OC=1+2=3,
∴当点C的坐标为(3,0)时,以A,E,C为顶点的三角形是等腰三角形.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=16,AD是BC边上的中线且AD=6,![]() 是AD上的动点,
是AD上的动点,![]() 是AC边上的动点,则
是AC边上的动点,则![]() 的最小值是( ).
的最小值是( ).

A.![]() B.16C.6D.10
B.16C.6D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(-2,1),B(-3,4),C(-1,3),过点(l,0)作x轴的垂线![]() .
.
(1)作出△ABC关于直线![]() 的轴对称图形△
的轴对称图形△![]() ;
;
(2)直接写出A1(___,___),B1(___,___),C1(___,___);
(3)在△ABC内有一点P(m,n),则点P关于直线![]() 的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).
的对称点P1的坐标为(___,___)(结果用含m,n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书,第一次用![]() 元购书若干本, 并按该书定价
元购书若干本, 并按该书定价![]() 元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了
元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了![]() ,他用
,他用![]() 元所购该书数量比第一次多
元所购该书数量比第一次多![]() 本.当按定价
本.当按定价![]() 元售出
元售出![]() 本时,出现滞销,便以定价的
本时,出现滞销,便以定价的![]() 折售完剩余的书.
折售完剩余的书.
![]() 每本书第一次的批发价是多少钱?
每本书第一次的批发价是多少钱?
![]() 试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:我们将能完全覆盖三角形的最小圆称为该三角形的最小覆盖圆.若三角形为锐角三角形,则其最小覆盖圆为其外接圆;若三角形为直角或钝角三角形,则其最小覆盖圆是以三角形最长边(直角或钝角所对的边)为直径的圆.问题:能覆盖住边长为![]() 、
、![]() 、
、![]() 的三角形的最小圆的直径是________.
的三角形的最小圆的直径是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
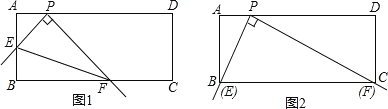
【题目】在矩形ABCD中,点P在AD上,AB=![]() ,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB、BC于点E、F,连接EF(如图1).当点E与点B重合时,点F恰好与点C重合(如图2).将直角尺从图2中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,从开始到停止,线段EF的中点所经过的路径长为.
,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB、BC于点E、F,连接EF(如图1).当点E与点B重合时,点F恰好与点C重合(如图2).将直角尺从图2中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,从开始到停止,线段EF的中点所经过的路径长为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假即将到来,外出旅游的人数逐渐增多,对旅行包的需求也将增多,某店准备到生产厂家购买旅行包,该厂有甲、乙两种新型旅行包.若购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元.
(1)甲、乙两种旅行包的进价分别是多少元?
(2)若该店恰好用了7000元购买旅行包;
①设该店购买了m个甲种旅行包,求该店购买乙种旅行包的个数;
②若该店将甲种旅行包的售价定为298元,乙种旅行包的售价定为325元,则当该店怎么样进货,才能获得最大利润,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com