Question

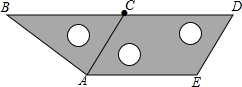
4．如图，将三个相同的三角板不重叠不留空隙地拼在一起，观察图形，在线段AB，BD，DE，EC，CA，AE中，相互平行的线段有（　　）

• A． 4组
• B． 3组
• C． 2组
• D． 1组

Answer 1

分析 在复杂的图形中具有相等关系或互补关系的两角首先要判断它们是否是同位角、内错角或同旁内角，被判断平行的两直线是否由“三线八角”而产生的被截直线．

解答 解：如图，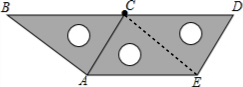

∠BAC=∠ACE=90°，则AB∥CE（内错角相等，两直线平行）；
∠ACE=∠CED=90°，则AC∥DE（内错角相等，两直线平行）；
∠AEC=∠ECD，则BD∥AE（内错角相等，两直线平行）；
所以在线段AB，BD，DE，EC，CA，AE中，相互平行的线段有AB∥CE、AC∥DE、BD∥AE这3组，
故选：B．

点评 本题是考查平行线的判定的基础题，比较容易，同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．