
分析 活动1:应用树状图法,判断出甲胜出的概率是多少即可.
活动2:首先对甲、乙、丙三名同学规定一个摸球顺序:丙→甲→乙,然后应用树状图法,判断出第一个摸球的丙同学和最后一个摸球的乙同学胜出的概率各等于多少即可.
猜想:首先根据(1)(2),猜想这三名同学每人胜出的概率之间的大小关系为:P(甲胜出)=P(乙胜出)=P(丙胜出);然后总结出得到的活动经验为:抽签是公平的,与顺序无关.
解答 解:活动1:画树状图得: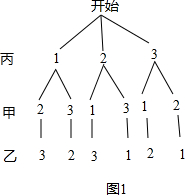 ,
,
∵共有6种等可能的结果,甲胜出的有2种情况,
∴P(甲胜出)=$\frac{1}{3}$.
活动2:对甲、乙、丙三名同学规定一个摸球顺序:丙→甲→乙;
画树状图得: ,
,
∵共有24种等可能的结果,第一个摸球的丙同学胜出的有6种情况,最后一个摸球的乙同学胜出的也有6种情况,
∴P(丙胜出)=$\frac{6}{24}$=$\frac{1}{4}$,P(乙胜出)=$\frac{6}{24}$=$\frac{1}{4}$.
故答案为:丙,甲,乙,$\frac{1}{4}$,$\frac{1}{4}$;
猜想:这三名同学每人胜出的概率之间的大小关系为:P(甲胜出)=P(乙胜出)=P(丙胜出).
得到的活动经验为:抽签是公平的,与顺序无关.(答案不唯一)
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:选择题
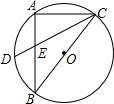 如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )
如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )| A. | 7:2 | B. | 5:2 | C. | 4:1 | D. | 3:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
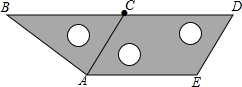 如图,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线段AB,BD,DE,EC,CA,AE中,相互平行的线段有( )
如图,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线段AB,BD,DE,EC,CA,AE中,相互平行的线段有( )| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com